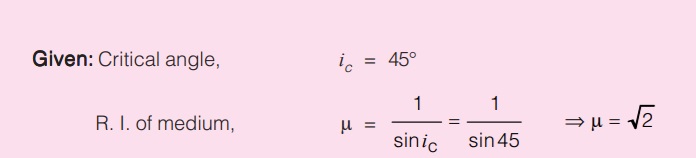Refraction of Light
When light moves through a uniform medium, it follows a straight trajectory. However, upon transitioning from one transparent medium to another, its path bends at the interface between the two substances, a phenomenon known as refraction.
The path along which the light travels in the first medium is called incident ray and that in the second medium is called refracted ray. The angles which the incident ray and the refracted ray make with the normal at the surface of separation are called angle of incidence (i) and angle of refraction (r) respectively.
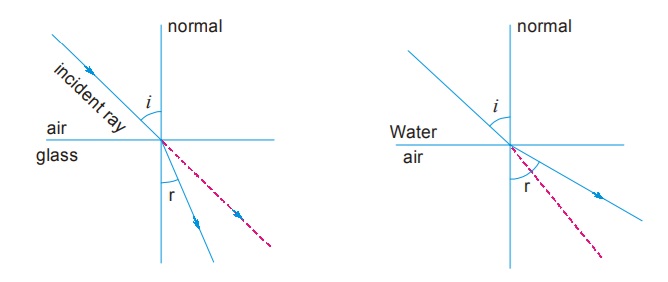
Observation of Refraction of Light:
- When a ray of light passes from an optically rarer medium to a denser medium, it bends towards the normal (∠i > ∠r)
- When a ray of light passes from an optically denser to a rarer medium, it bends away from the normal (∠r > ∠i)
- A ray of light travelling along the normal passes without any deflection, ∠i = ∠r = 0°.
Table of Contents
- Observation of Refraction of Light
- Effects of Refraction
- Laws of Refraction
- The Refractive Index
- Apparent Depth and Real Depth
- Refraction Through a Rectangular Glass Slab
- Calculation of Lateral displacement
- Refraction Through Compound Slab
- Refraction Through Compound Slab: Example and Solution
- Total Internal Reflection
- Total Internal Reflection: Example and Solution
Reason behind Refraction:
- The cause of refraction of light lies in the change of speed that occurs when light passes from one transparent medium to another of different optical density.
- When light travels from a less dense medium (e.g., air) to a denser one (e.g., glass or water), it slows down. Conversely, when it moves from a denser medium to a less dense one, it speeds up.
- This change in speed leads to a change in the direction of light’s propagation at the boundary between the two mediums.
- According to Snell’s Law, this change in direction is determined by the difference in optical densities of the two mediums.
- In essence, refraction occurs because light waves change speed and direction as they move from one medium to another.
Note:
- The frequency of the refracted ray remains unchanged.
- The intensity of the refracted ray is less than that of the incident ray. It is because there is partial reflection and absorption of light at the interface.
Effects of Refraction:
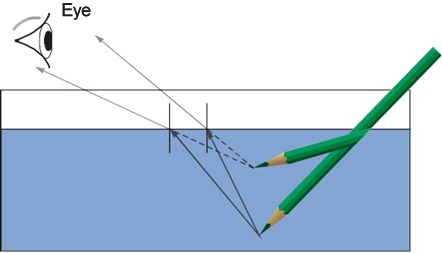
- A pencil appears bent and short in water:
The pencil appears bent and shorter in water due to the refraction of light. Light bends as it passes from water to air, causing the pencil to appear displaced from its actual position. This bending of light makes the pencil seem bent at the water’s surface and shorter overall when viewed from above.
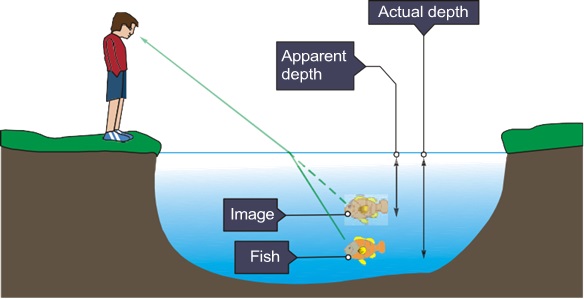
- A water tank appears shallow e. less deep than its actual depth:
The water tank appears shallower than its actual depth due to the phenomenon of refraction. When light travels from water to air, it bends due to the change in optical density between the two mediums. This bending causes the objects submerged in water to appear displaced from their actual positions. As a result, the bottom of the water tank appears closer to the surface than it really is, creating the illusion that the tank is shallower than it truly is.
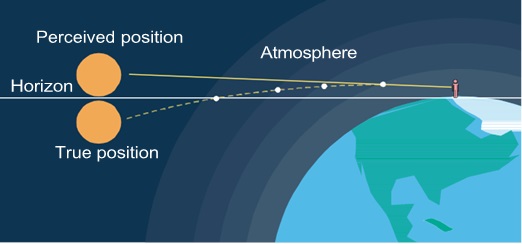
- Apparent shift in the position of the sun at sunrise and sunset:
The apparent shift in the position of the sun at sunrise and sunset is due to the refraction of light in the Earth’s atmosphere. As the sun rises or sets, its light travels through a thicker layer of the Earth’s atmosphere near the horizon.
This dense atmosphere causes the sunlight to bend or refract, making the sun appear slightly higher in the sky than it actually is when rising and setting.
This phenomenon causes the sun to appear displaced from its true position, leading to the apparent shift in its position at sunrise and sunset.
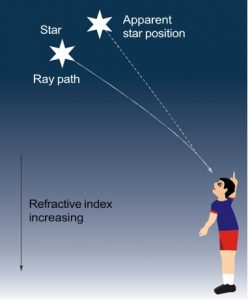
- Twinkling of stars:
The twinkling of stars is caused by the refraction of starlight as it passes through the Earth’s atmosphere. The atmosphere is not uniform; it consists of layers of air with different temperatures and densities. When starlight enters the Earth’s atmosphere, it encounters these varying layers, bending the light rays slightly. As a result, the apparent position of the star appears to shift slightly, creating the twinkling effect. Factors such as turbulence and air currents in the atmosphere further contribute to the twinkling by causing rapid fluctuations in the density and temperature of the air, which in turn cause the starlight to vary in intensity.
Laws of Refraction:
There are two laws of refraction:- The incident ray, the refracted ray and the normal at the point of incidence lie in the same plane.

Laws of refraction are valid for both types of surfaces i.e. for plane as well as spherical refracting surfaces.
The Refractive Index:
- Refractive Index in terms of Speed of Light: The refractive index of a medium for a light of given wavelength may be defined as the ratio of the speed of light in vacuum to its speed in that medium.

- Refractive Index in terms of Wavelength: Since the frequency (f ) remains unchanged when light passes from one medium to another, therefore,
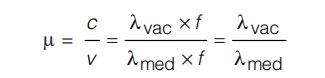
The refractive index of a medium may be defined as the ratio of wavelength of light in vacuum to its wavelength in that medium.
- Relative Refractive Index: The relative refractive index of medium 2 with respect to medium 1 is defined as the ratio of speed of light (v1) in the medium 1 to the speed of light (v2) in medium 2 and is

- Factors on which the refractive index of a medium depends are:
- Nature of the medium.
- Wavelength of the light used.
- Temperature.
- Nature of the surrounding medium.
It may be noted that refractive index is a characteristic of the pair of the media and also depends on the wavelength of light, but is independent of the angle of incidence.
- Physical significance of refractive index: The refractive index of a medium gives the following information:
- The refractive index provides insight into the direction of bending for a refracted ray, indicating whether it will bend towards or away from the normal.
- The refractive index of a medium is tied to the speed of light, expressed as the ratio of the speed of light in a vacuum to its speed in the given medium. For instance, if the refractive index of glass is stated as 3/2, it signifies that the speed of light in glass is two-thirds of its speed in a vacuum
| Material Medium | Refractive index |
|---|---|
| Air | 1.0003 |
| Ice | 1.31 |
| Water | 1.33 |
| Alcohol | 1.36 |
| Kerosene | 1.44 |
| Fused quartz | 1.46 |
| Turpentine oil | 1.47 |
| Benzene | 1.50 |
| Material medium | Refractive index |
|---|---|
| Crown glass | 1.52 |
| Canada Balsam | 1.53 |
| Rock salt | 1.54 |
| Carbon disulfide | 1.63 |
| Dense flint glass | 1.65 |
| Ruby | 1.71 |
| Sapphire | 1.77 |
| Diamond | 2.42 |
Apparent Depth and Real Depth:
The extent to which the bottom of tank appears to be raised depends upon the value of refractive index of the refracting medium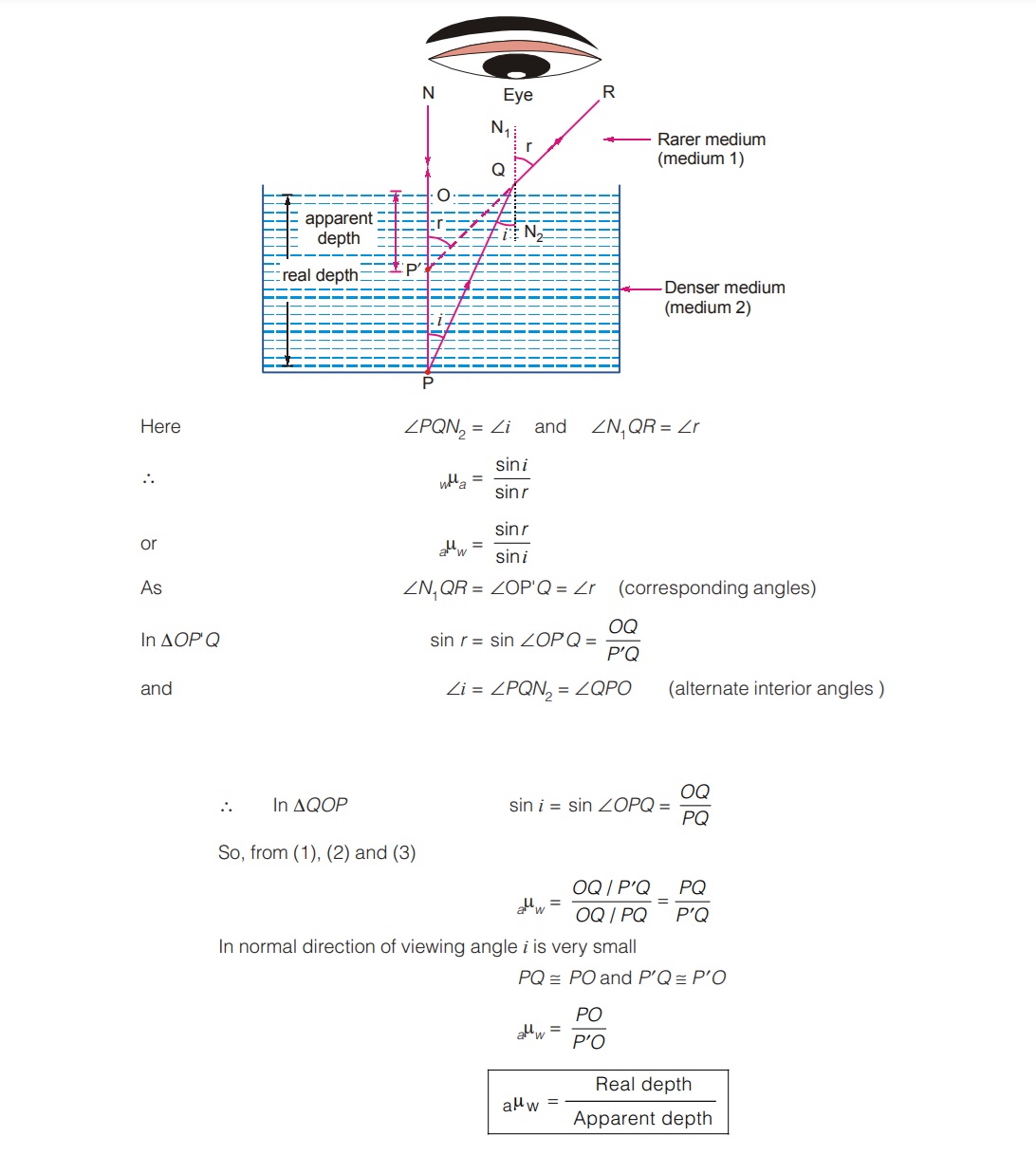
Refraction Through a Rectangular Glass Slab:
A ray AE is incident on the face PQ at an angle of incidence i. On entering the glass slab, it bends towards normal and travels along EF at an angle of refraction r. The refracted ray EF is incident on face SR at an angle of incidence r’. The emergent ray FD bends away from the normal at an angle of refraction e.
Thus the emergent ray FD is parallel to the incident ray AE, but it has been laterally displaced with respect to the incident ray. There is shift in the path of light on emerging from a refracting medium with parallel faces.
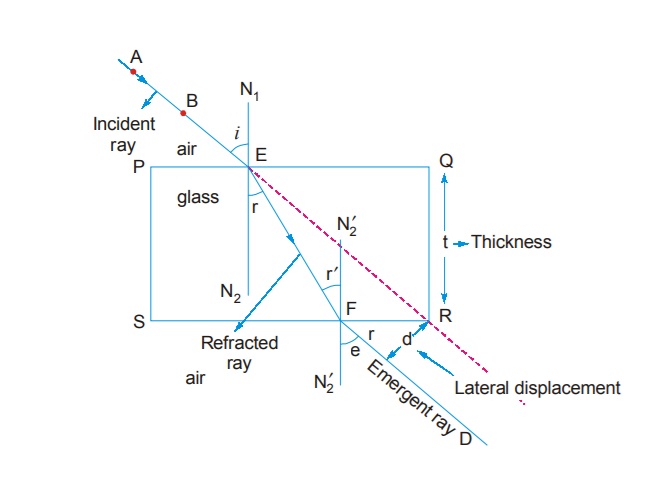
Calculation of Lateral displacement:
Lateral displacement is the perpendicular distance between the incident and emergent rays when light is incident obliquely on a refracting slab with parallel faces.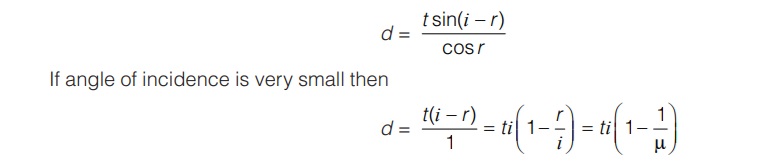 Factors on which lateral shift depends are:
Factors on which lateral shift depends are:
- Lateral shift is directly proportional to the thickness of glass slab.
- Lateral shift is directly proportional to the incident angle.
- Lateral shift is directly proportional to the refractive index of glass slab.
- Lateral shift is inversely proportional to the wavelength of incident light.
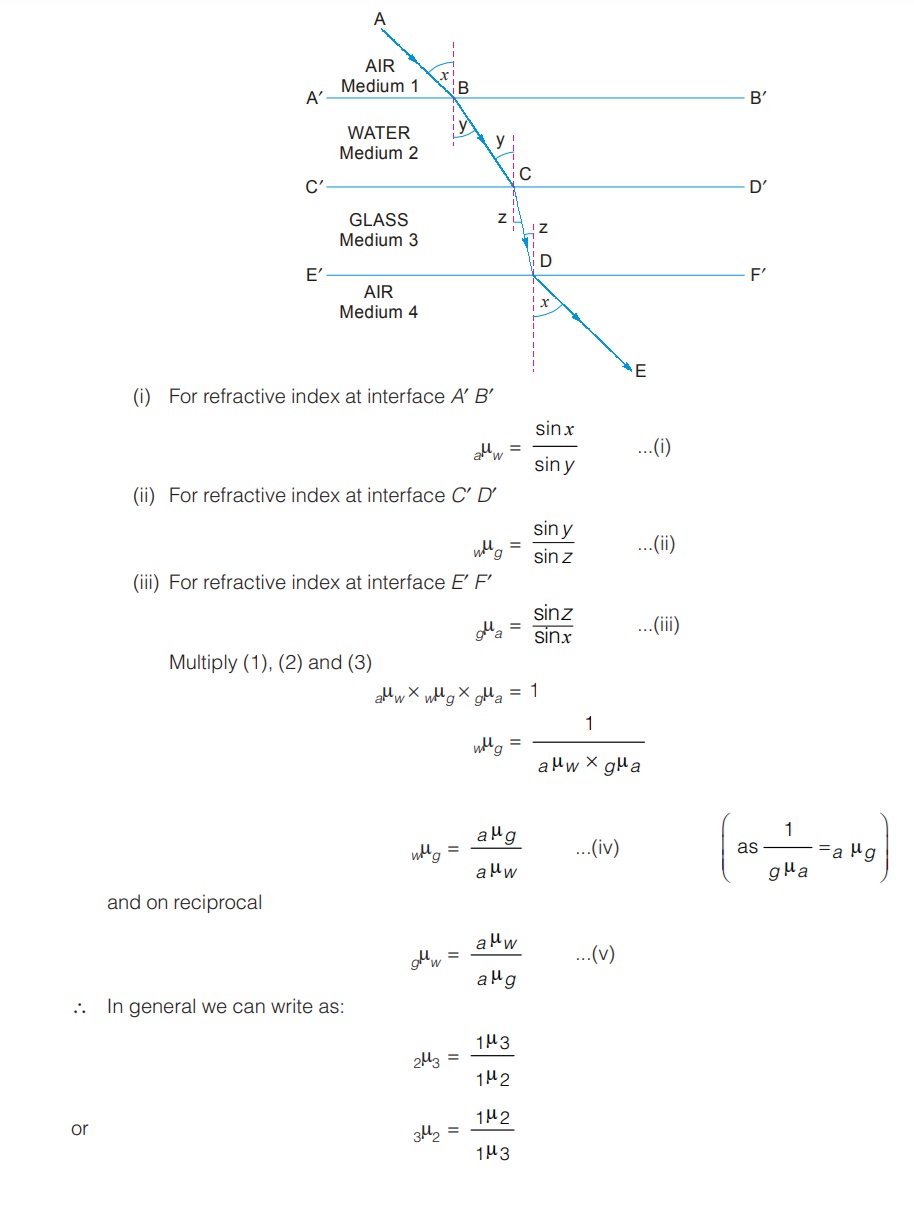
Refraction Through Compound Slab:
Example :
Calculate the speed and wavelength of light (i) in glass and (ii) in air, when light waves of frequency 6 × 1014 Hz travel from air to glass of μ = 1.5.Solution :

Example :
The depth of water in a tank is 4 meter. If the refractive index of water is 4/3 , by how much distance does the bottom of tank appear to be raised?Solution :
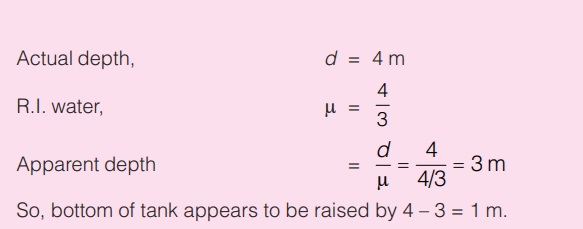
Example :
A ray of light travelling in air is incident on the plane surface of a transparent medium. The angle of incidence is 45° and the angle of refraction is 30°. Find the refractive index of the medium.Solution :
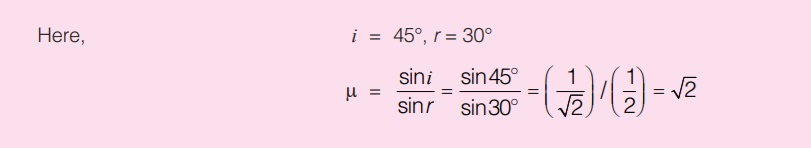
Example :
A ray of light travelling in air falls on the surface of a rectangular slab of a plastic material whose refractive index is 1.6. If the incident ray makes an angle of 53° with the normal, find the angle made by the refracted ray with the normal (sin 53° = 4/5).
Solution :

Example :
Find the refractive index of glass with respect to water. The refractive indices of these with respect to air are 3/2 and 4/3 respectively.Solution :
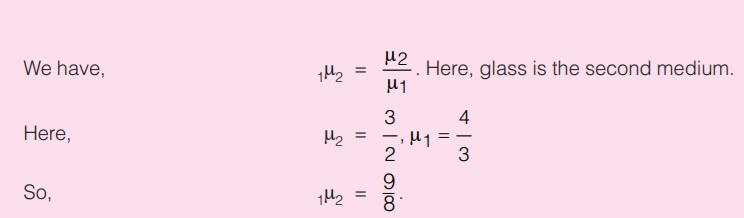
Total Internal Reflection:
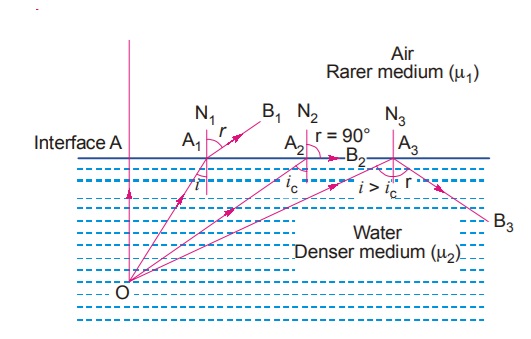
Total internal reflection occurs when a ray of light traveling from a denser to a rarer medium is reflected back into the denser medium, given that it strikes the interface between the two mediums at an angle exceeding the critical angle.
As the angle of incidence increases, the refracted ray bends towards the interface. At a particular angle of incidence, the, refracted light travels along the interface and the angle of refraction becomes 90°.
The angle of incidence for which angle of refraction becomes 90° is called critical angle ic.

When the angle of incidence becomes greater than the critical angle, there is no refracted light and all the light is reflected back. This phenomenon is known as total internal reflection.
Conditions for total Internal Reflection:
- The light should travel from denser to rarer medium.
- The angle of incidence must be greater than the critical angle for the given pair of media.
Important points in T.I.R.
- During total internal reflection of light, the whole incident light energy is reflected back to the same optically denser medium.
- Greater the wavelength, greater will be the critical Thus, critical angle of a medium will be maximum for red colour and minimum for violet colour.
- Image formed due to total internal reflection is much brighter because total light is reflected back into the same medium and there is no loss in intensity of light.
Example:
If critical angle for a medium is 45°, then find the refractive index of the medium.
Solution: