Ampere’s Circuital Law
This law is useful in finding the magnetic field due to currents under certain conditions of symmetry. Consider a closed plane curve enclosing some current-carrying conductors.

Where I = total current (algebraic sum) crossing the area.

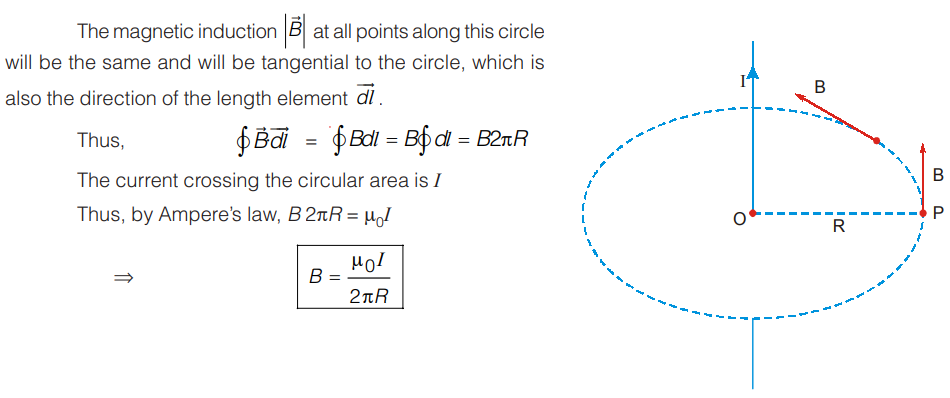
As a simple application of this law, we can derive the magnetic induction due to a long straight wire carrying current I.
Suppose the magnetic induction at point P, distant R from the wire is required.
Draw the circle through P with centre O and radius R.
Example :
Write equation for Ampere’s circuital law for the Amperian loop shown (traversed in the direction shown by arrow marks put on it).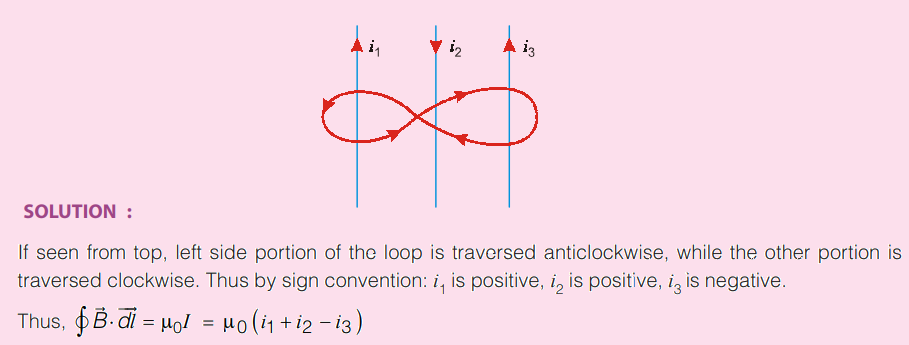
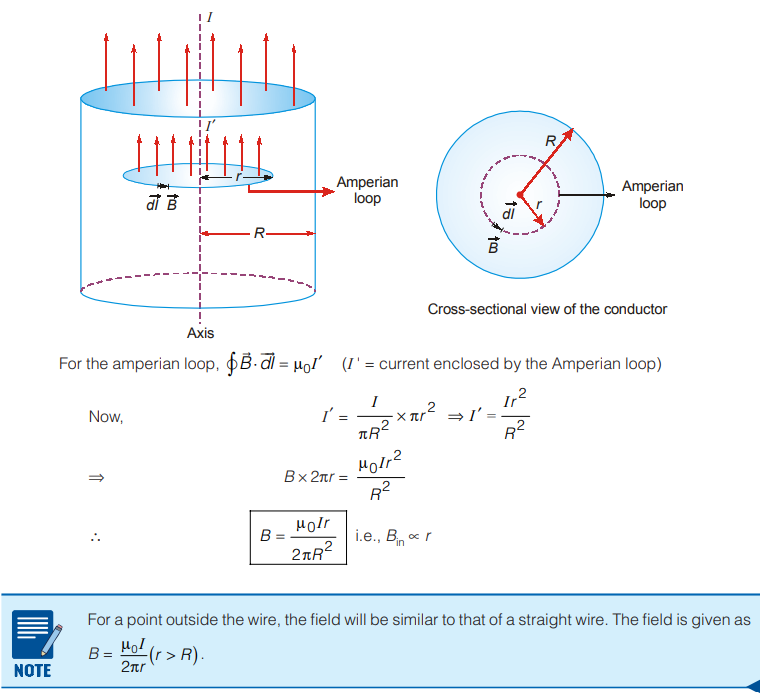
Magnetic field inside a long straight current carrying conductor (at a point distant r from axis of the conductor)
Again, we choose a loop of radius r as Amperian loop and choose direction of integration as anticlockwise.
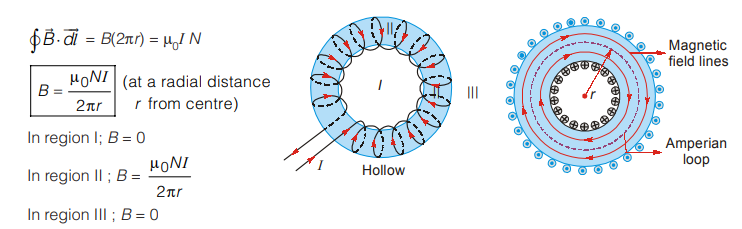
Magnetic Field Inside a Hollow Straight Current Carrying Conductor (at a Distance r from Axis of the Loop)
For the chosen Amperian loop (or radius r), current enclosed is zero.
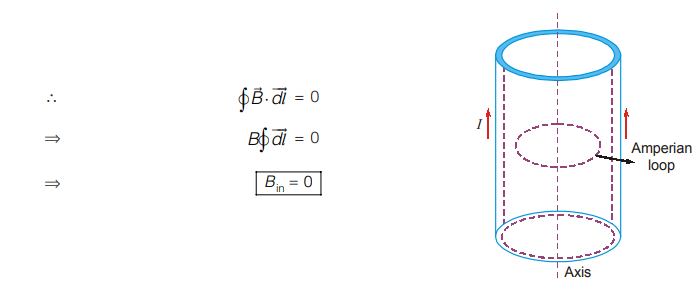
Hence, there is no magnetic field inside a hollow current carrying conductor.
Magnetic Field Due to An Infinite Plane Sheet of Current
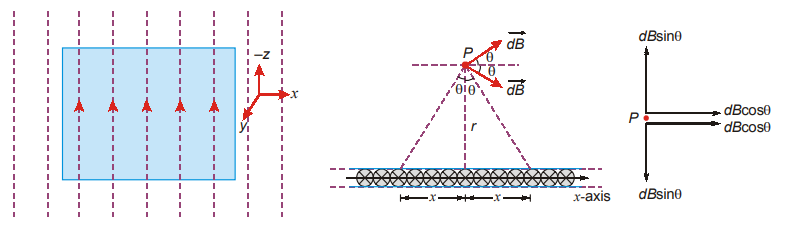
An infinite sheet of current lies in x-z plane, carrying current along – z-axis. The field at any point P on y-axis is along a line parallel to x-z plane. We can take a rectangular Amperian loop as shown. If you traverse the loop in clockwise direction, inward current will be positive, by sign convention.
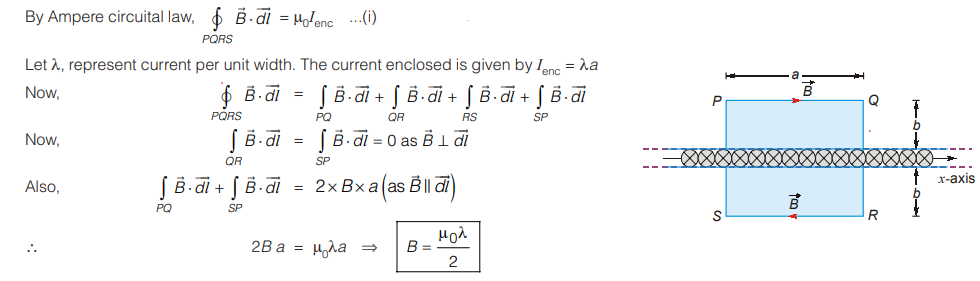
Example :
Consider a system of two long coaxial cylinders : Solid (of radius a carrying i current in positive z direction) and hollow (of radius b carrying current i in negative z direction). Find the magnetic field at a point distant r from axis of the cylinders for- r ≤ a
- a < r < b
- r ≥ b
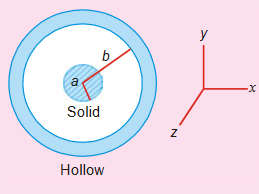
Solution :

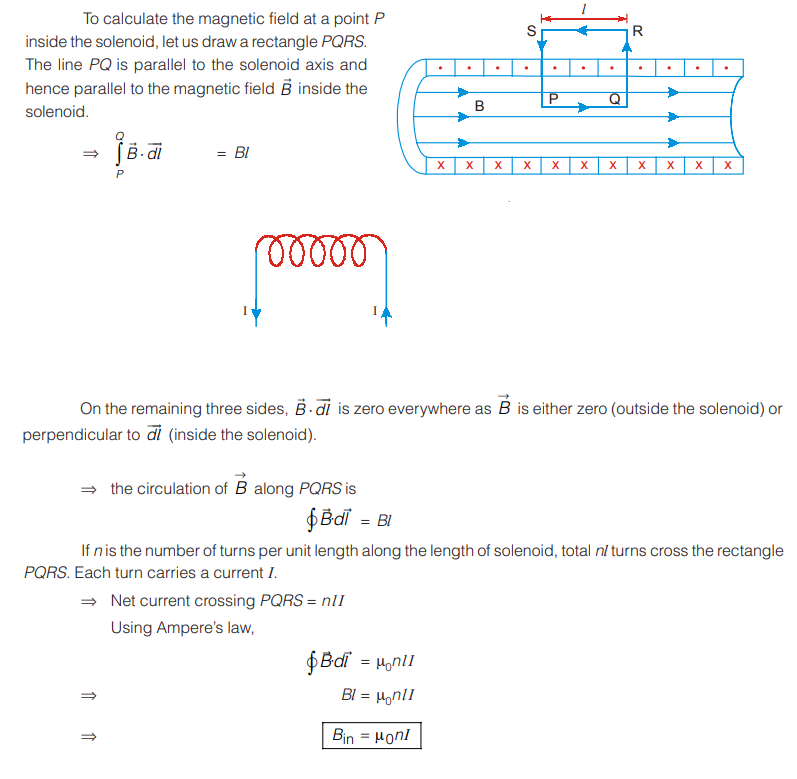
Magnetic Field Inside a Long Solenoid
A solenoid is a wire wound closely in the form of a helix, such that the adjacent turns are electrically insulated.
The magnetic field inside a very tightly wound long solenoid is uniform everywhere along the axis of the solenoid and is zero outside it.
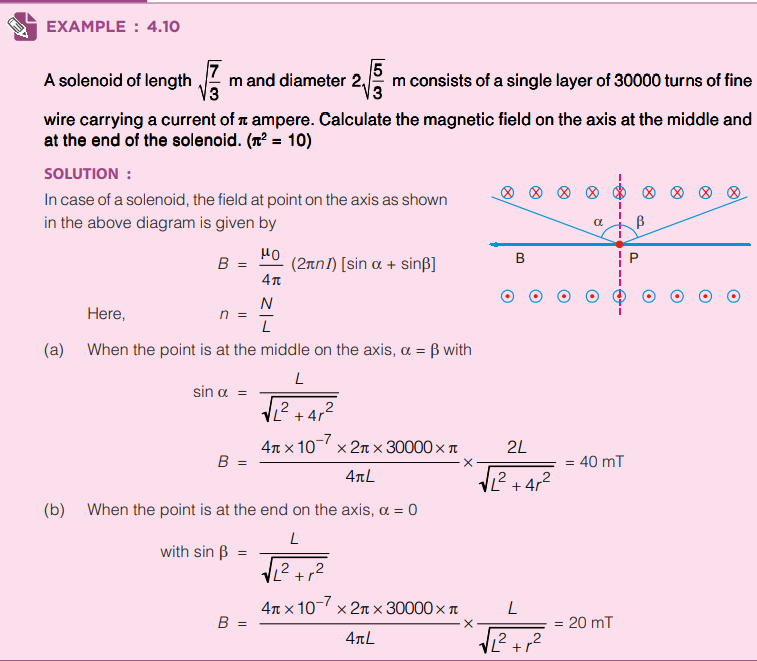
Magnetic Field at a Point on The Axis of a Short Solenoid
Consider a solenoid of length l and radius R containing N closely spaced turns and carrying a steady current I. We have to find out an expression for the magnetic field at an axial point P lying in the space enclosed by the solenoid as shown in the figure below.
The field at a point on the axis of a solenoid can be obtained by the superposition of fields due to a large number of identical coils all having their centre on the axis of the solenoid.
Let us consider a coil of width dx at a distance x from the point P on the axis of the solenoid. The field at P due to this coil is given by
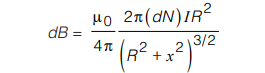
If n be the number of turns per unit length, dN = ndx.
From the above figure,
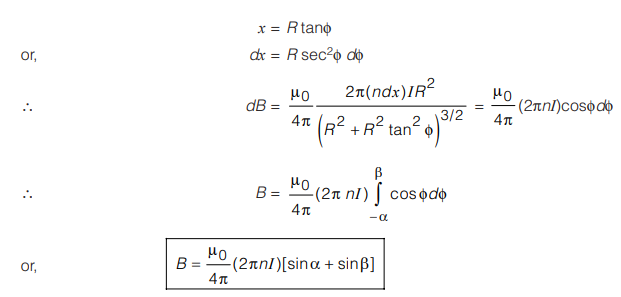
Now consider some cases involving the application of above equation.
Case I : If the solenoid is of infinite length and the point is well inside the solenoid, 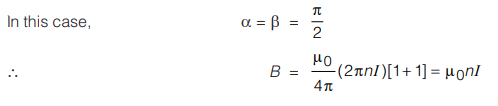
Case II : If the solenoid is of infinite length and the point is near one end
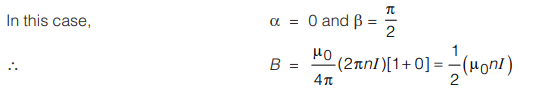
Case III : If the solenoid is of finite length and the point is on the perpendicular bisector of its axis
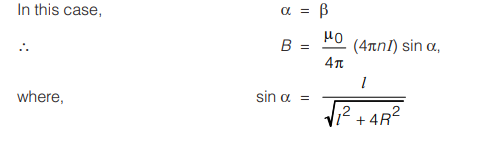
Magnetic Field of a Toroid
A toroid is a solenoid bent to form a ring. Let N be the total number of turns. For an Amperian loop of radius r,