Circular Motion

Edited By: MENIIT Team | Updated on Jul 17, 2024 10:00 AM GMT+0000 | # Physics

For a body moving in a circle of radius R with uniform speed v centripetal acceleration,

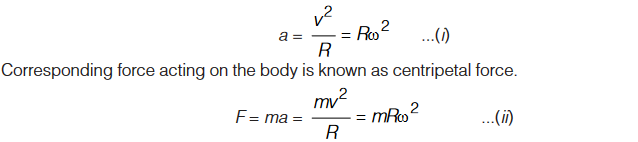
This force acts along the radius and towards the centre of the circle.

For a stone moving in circular path, the centripetal force is provided by tension in the string.

For planets moving around the sun, gravitational force provides the necessary centripetal force.

For a car taking a circular turn on a horizontal road, frictional force provides the centripetal force.

Let us study applications of the laws of motion on the horizontal circular motion.

Table of Contents

Motion of a Car on a Level Road

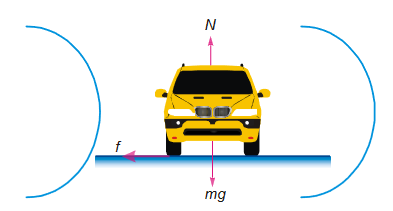
When a car is moving on a level road, forces acting on the car are :

Its weight, mg
Normal reaction, N
Frictional force, f(along the surface of the road, towards the centre of the turn)

N – mg = 0 N = mg …(I)

Frictional force, or the component of the contact force between road and the tyres along the surface provides the necessary centripetal force. It is the static friction that provides the centripetal acceleration. It opposes the impending motion of the car moving away from the circle.

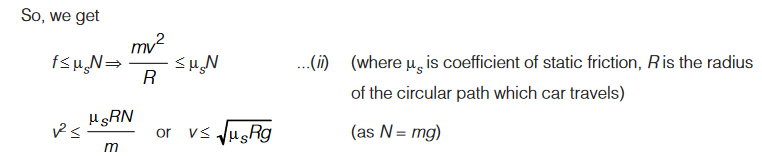
Note that this expression is independent of the mass of the car.

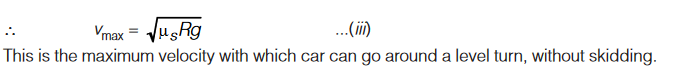
Example :

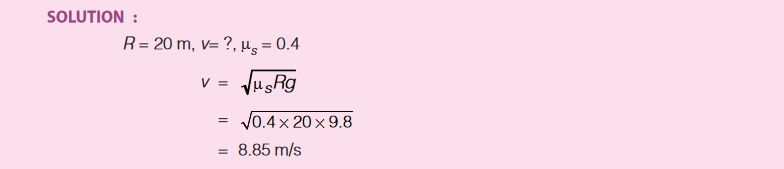
Find the maximum speed with which a car can turn on a bend without skidding, if radius of bend is 20 m and coefficient of friction between the road and the tyres is 0.4. solution

Example :

A cyclist speeding at 4.5 km/h on a level road takes a sharp circular turn of radius 3 m without reducing the speed. The coefficient of static friction between the road and the tyres is 0.1.

(i) Will he slip while taking the turn?

(ii) Will he slip if his speed is 9 km/h?

SOLUTION:

Frictional force provides the necessary centripetal force. He will slip if his speed is large, than the safe speed of turning. Maximum speed for not slipping is example 3

Motion of a car on a banked road

Motion of a car on a rough banked road

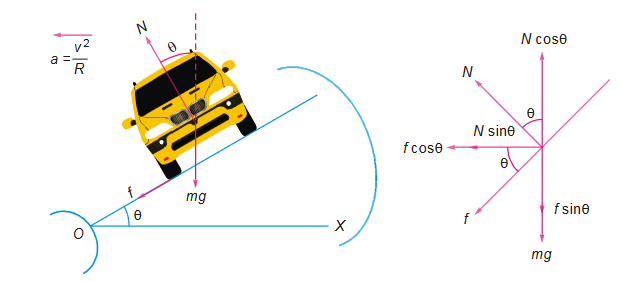
If we want to increase the maximum possible speed then the road should be banked as shown in the figure (this is the phenomenon of raising outer edge of the curved road above the inner edge) by this we can reduce the contribution of friction to the circular motion of the car.

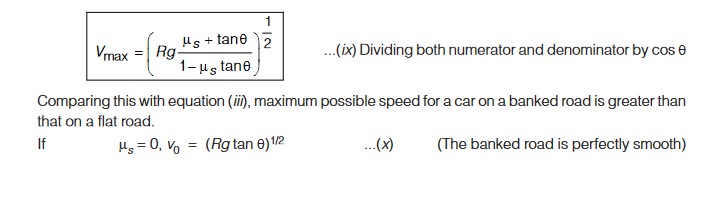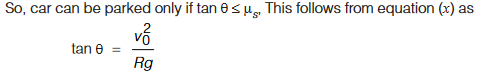
formula This speed is known as optimum speed. At this speed, frictional force is not required at all to provide centripetal force. Driving at this speed causes little wear and tear of the tyres. If speed of car is less than this, frictional force will be up the slope. formula

Example :

A circular racetrack of radius 100 m is banked at an angle of 45°. What is the

(i) Optimum speed of race car to avoid wear and tear of its tyres?

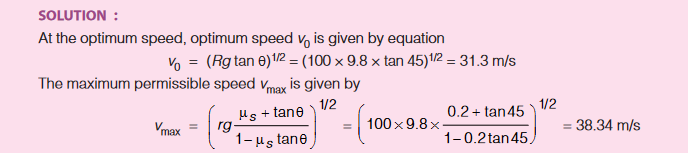
(ii) Maximum permissible speed to avoid slipping if the coefficient of friction is 0.2? solution

Non Uniform Circular Motion

When a particle is moving in a circle with changing speed (v), in addition to the centripetal acceleration v²/r, a tangential acceleration a_t = dv/dt is also a component of the acceleration “a” of the particle. That is

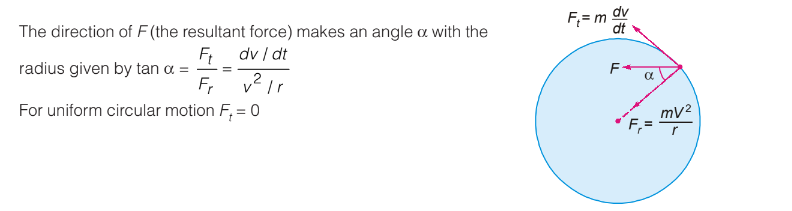
Consider the statement : “The force acting on a particle moving on a circular path is centripetal”. This statement is true only when the speed of the particle is constant. The correct statement should be like this,

“There must be a centripetal component of the force acting on the particle moving on a circular path”.

The tangential component of the force acting on the particle moving on a circular path is nonzero only when the speed is changing otherwise it is zero.

Example :

A car starts from rest on a horizontal circular road of radius 190 m and gains speed at a uniform rate of 1.2 m/s², The coefficient of static friction between the road and the tyres is 0.37. Calculate the distance travelled by the car before it begins to skid.