Gauss’s Law
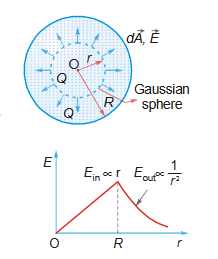
Gauss law relates the flux through a closed surface (a surface that encloses some volume) with charges present inside the surface.“ Consider a point charge q surrounded by a spherical surface of radius r centered on the charge. The magnitude of the electric field everywhere
on the surface on the sphere is E = k q/r24
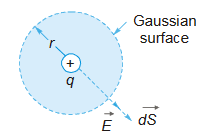
The electric field is perpendicular to the spherical surface at all points on the surface. The electric flux through the surface is therefore EA, where A = 4πr² is the surface area of the sphere:


Example :
Find out flux through the given Gaussian surface.
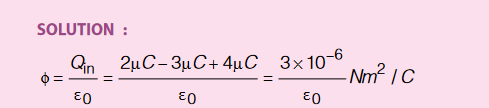
Example :
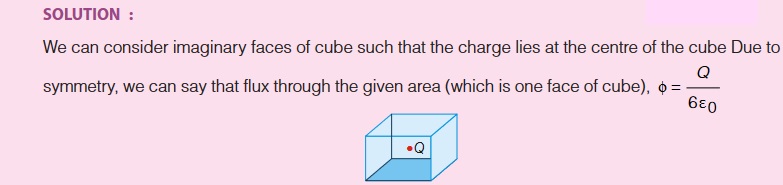
If a point charge q is placed at the centre of a cube, then find out flux through any one face of cube.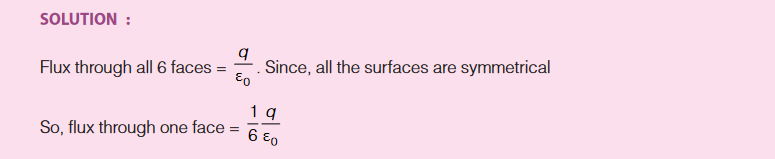
Applications of Gauss’s Law
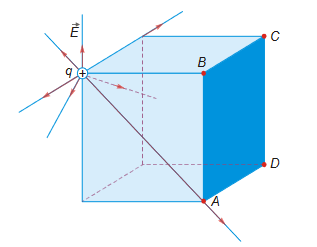
Calculation of flux through surface ABCD by usage of symmetry :
(a) A charge q is placed at the corner of a cube
(b) By surrounding the charge with a series of cubes (total 8 cubes) such that the charge is at the centre of a larger cube, we have created an arrangement sufficiently symmetric to be able to solve for desired flux values.


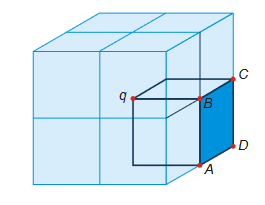
Example :
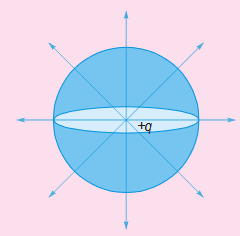
A point charge +q is placed at the centre of curvature of a hemisphere. Find flux through the hemispherical surface.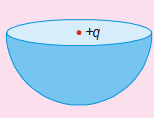

Example :
A charge Q is placed at a distance a/2 above the centre of a horizontal, square surface of edges as shown in figure. Find the flux of the electric field through the square surface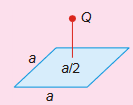
Selection of Gaussian Surface to calculate Electric Field :
With the help of extensive integration and considering a system which possess spherical, cylindrical or planar symmetry we can calculate electric field by Gauss law.
| System | Gaussian Surface |
|---|---|
| Point charge, Hollow Sphere, Solid Sphere | Spherical |
| Infinite Wire, Infinite Hollow Cylinder, Infinite Solid Cylinder | Cylindrical |
| Infinite Sheet | Gaussian Pillbox |
Let us understand how to apply Gauss Law with different cases :
Field due to a Point Charge
First, we shall look for the symmetry of the field. Clearly the field is spherically symmetric. If we enclose the charge in a sphere of radius R, the magnitude of electric field will be same at any point on the surface.
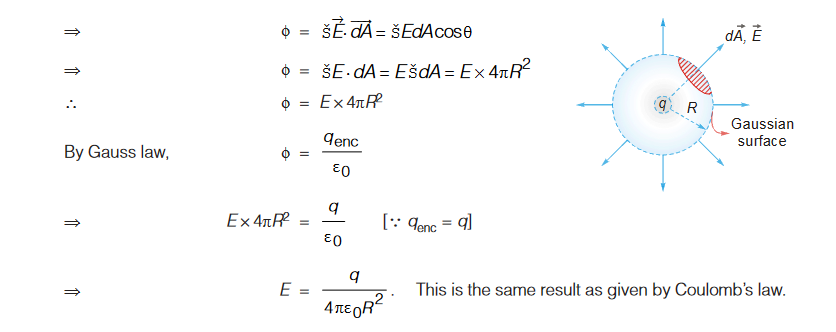 Field due to an infinitely long straight uniformly charged wire
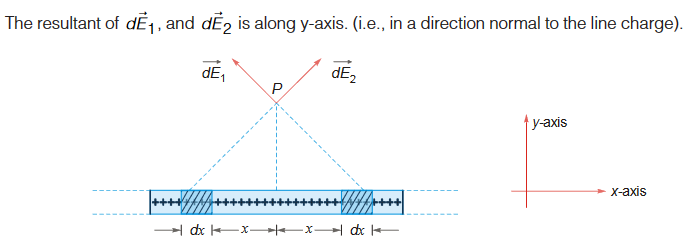
Field due to an infinitely long straight uniformly charged wire
First, we shall look for the symmetry of electric field. Consider any point P. at a distance r from the line charge.
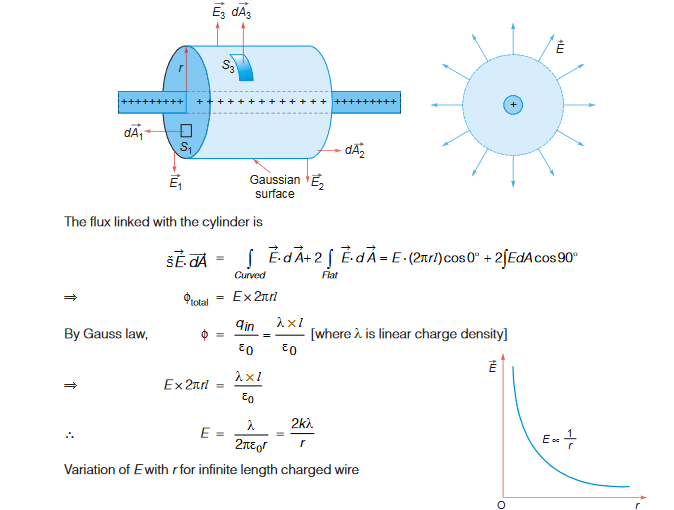
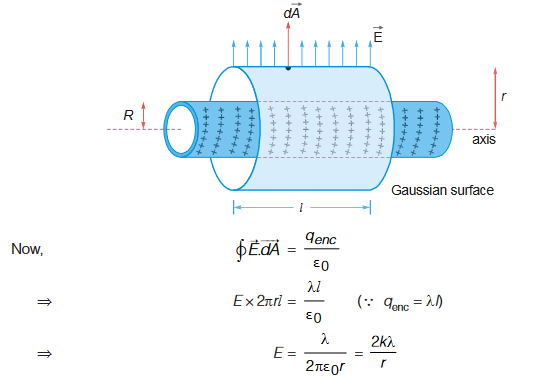
If a long linear charge distribution is kept along x-axis, at any point, field is directed radially away from x-axis. The field has a cylindrical symmetry. To find electric field, we enclose the distribution in a Gaussian cylinder of radius r and length l
Field due to Long uniformly charged Hollow Cylinder of Charge
Hollow cylinder with charge per unit length λ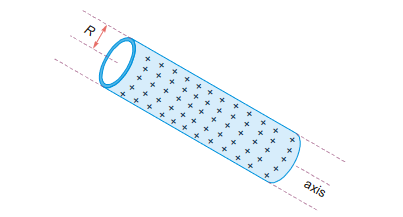 (a) Inside the cylinder (radial distance r < R):
(a) Inside the cylinder (radial distance r < R):
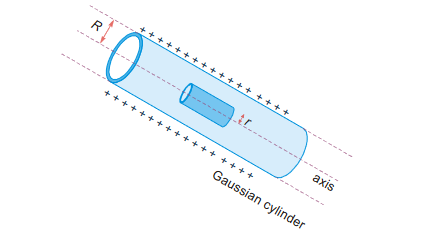
When we draw a Gaussian cylinder of radius r, we find that the charge enclosed by it is zero.
(b) Outside the cylinder (radial distance r > R) :
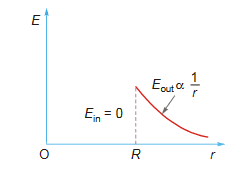
Variation of E with r is also shown graphically here.
Field due to Long uniformly charged Solid Cylinder of Charge
Let ρ be the volumetric charge density and R be the radius of the cylinder. Here, the field is radially away from x-axis having a cylindrical symmetry.
Case 1: r > R. Consider a Gaussian cylinder of length / and radius r about x-axis. Electric field lines are directed radially away. Let E be the magnitude of electric field, then φ = E × 2πrl
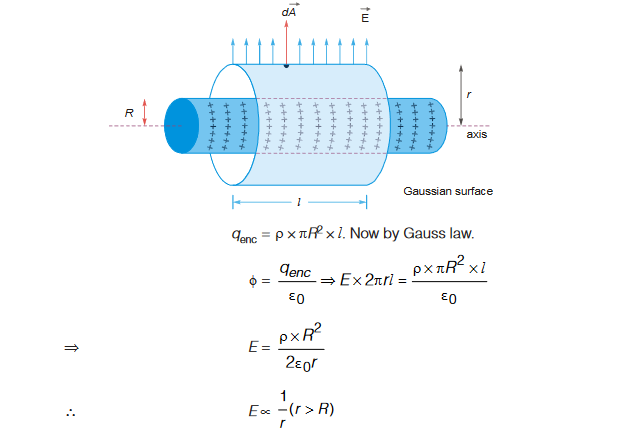
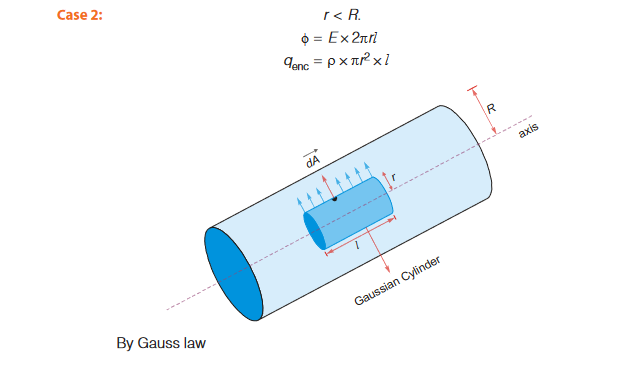
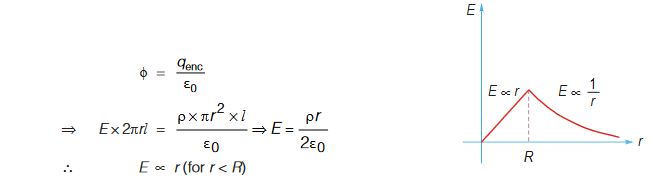
Field due to a uniformly charged thin spherical shell
Consider a shell having a charge Q uniformly distributed on its surface. The surface charge density is σ.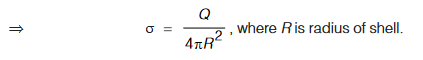
Field outside the shell:
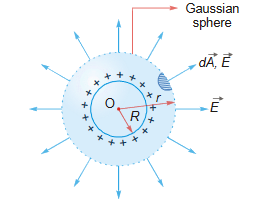
Case 1: Field outside the shell (radial distance r > R) We enclose the shell in a Gaussian sphere.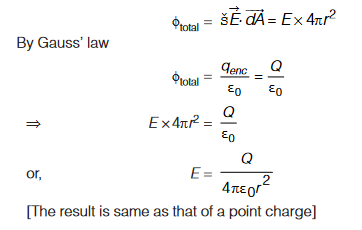
Field inside the shell:
Case 2: Field inside the shell (radial distance r < R)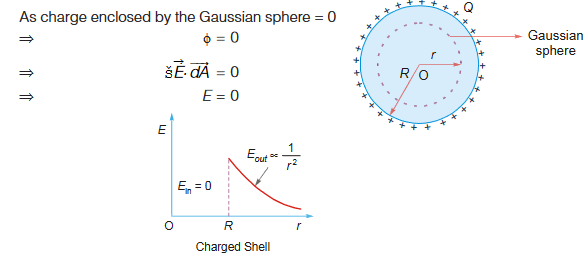
Field due to a uniformly charged Solid Sphere
Consider a uniform spherical charge distribution in which a charge Q is uniformly distributed over the volume of a sphere of radius R. The volumetric charge density is given by,
Field outside the shell :
Case 1: Field outside the sphere (radial distance r > R). The field has spherical symmetry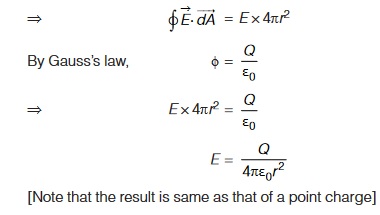
Field inside the shell :
Case 2 : Field inside the sphere (radial distance r < R). Consider a Gaussian sphere inside the sphere of charge.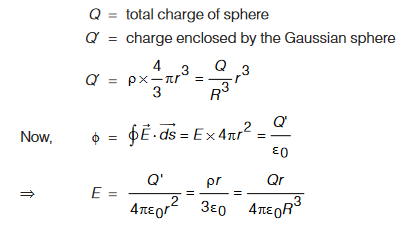
 Field due to a uniformly charged infinite plane sheet
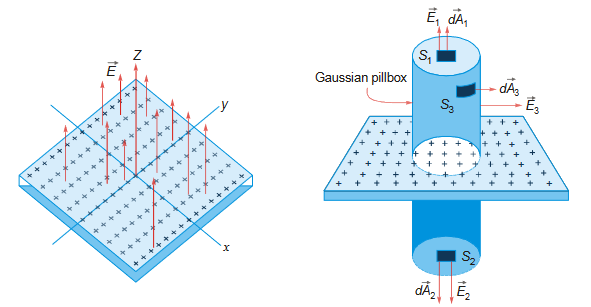
Field due to a uniformly charged infinite plane sheet
Non Conducting Sheet : Charge will be uniformly distributed on both the sides of the sheet. For Conducting sheets calculation will be different and we will learn that in Electrostatics of Conductors. 1. An infinitely large plane possesses a planar symmetry 2. Since the charge is uniformly distributed on the surface, the electric field must point perpendicular
We choose our Gaussian surface to be a cylinder, which is often referred to as a “pillbox”. The pillbox all consists of three parts, two end-caps s1 and s2 and a curved side s3.
 3. Since the surface charge distribution is uniform the charge enclosed by the Gaussian “pillbox” is qenc = σA where
A = A1 = A2 is the area of the end-caps.
4. The total flux through the Gaussian pillbox is
3. Since the surface charge distribution is uniform the charge enclosed by the Gaussian “pillbox” is qenc = σA where
A = A1 = A2 is the area of the end-caps.
4. The total flux through the Gaussian pillbox is
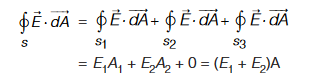
Since the two ends are at the same distance from the plane, by symmetry, the magnitude of the electric field must be the same : E1 = E2 = E. Hence, the total flux can be rewritten as φE= 2EA
5. By applying Gauss’s law, we obtain


Application :
Two parallel sheets are given surface charge densities σ1 and σ2. Electric fields in different regions are as shown
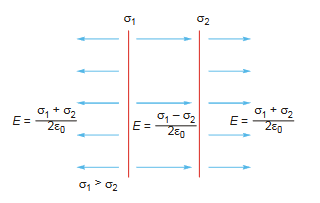
Consider the following specific cases : (i) When σ1 = σ, σ2 = σ, the situation will be like the one shown below
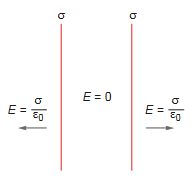
(ii) When σ1 = σ, σ2 = – σ, the situation will be like the one shown below
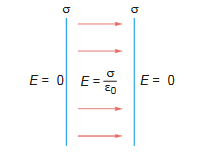
Example :
Two concentric shells of radii a and b carry charge q1 and q2 (uniformly distributed) respectively (a < b). Calculate electric field at radial distance r from the centre for (i) r < a (ii) b > r > a (iii) r > b. Represent this field graphically.Solution :
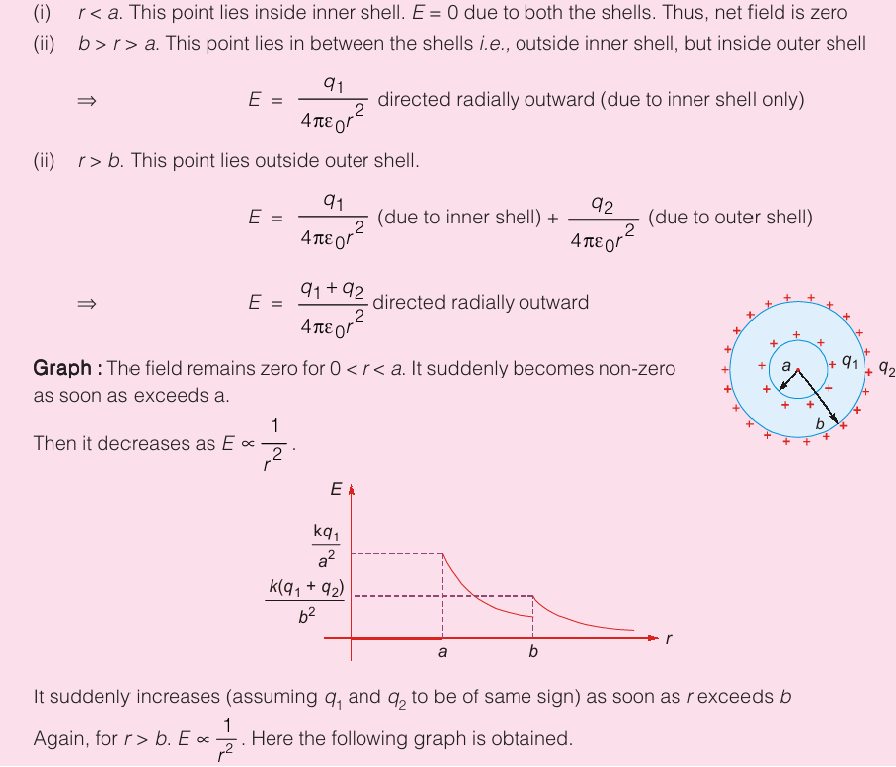
Example :
Figure shows a long thread along the axis of a long hollow cylinder. The charge per unit length of thread is λ, while that of the cylinder is λ, The radius of cylinder is R. What is the electric field at radial distance r from the axis for (i) r < R (ii) r > R?Solution :
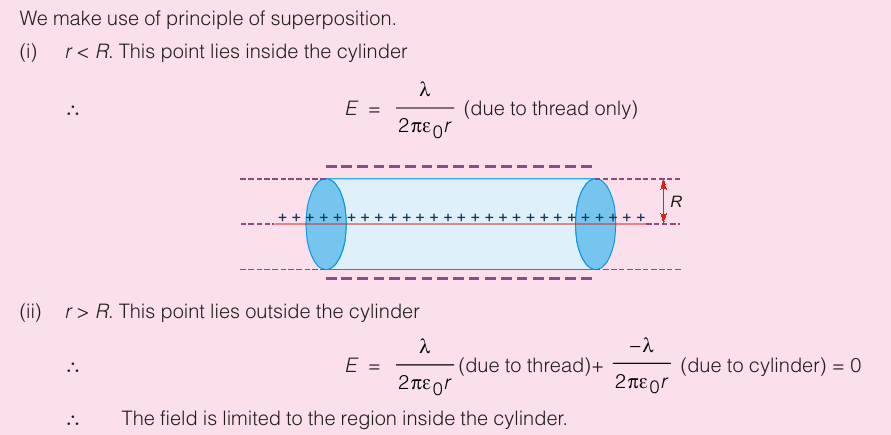
Example :
A large plane conducting sheet is given a charge so that its surface charge density becomes σ. Describe the electric field produced by it, inside the sheet and outside the sheet.Solution :