Motion in a Plane
Motion In Two Dimension
The motion of an object is called two dimensional, if two of the three co-ordinates are required to specify the position of the object in space changes w.r.t time.
In such a motion, the object moves in a plane. For example, a billiard ball moving over the billiard table, an insect crawling over the floor of a room, earth revolving around the sun etc.
Two special cases of motion in two dimension are (i) Projectile motion, (ii) Circular motion
Motion in a Plane
For the simplicity let’s consider two mutually perpendicular directions to study the planar motion as x-axis and y-axis.
At any time t particle is at (x, y) and after an infinitesimally small interval of time dt particle reaches to (x + dx, y + dy) coordinates.
dx and dy are the horizontal (x-axis) and vertical (y-axis) components of the displacement.
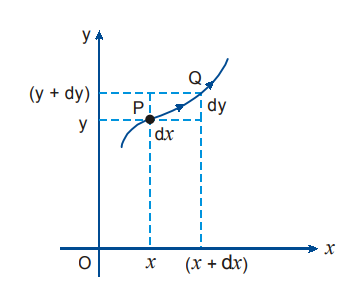

As we have learnt in vectors that two mutually perpendicular directions are independent of each other. None of them will have any impact on each other. So we can study the motion in a plane as superposition of two separate motions one along x-axis and another along y-axis. For solving problems in motion in a plane we apply equations of motion separately along x-axis and y-axis.
PROJECTILE MOTION
Types of Projectile Motion
- Oblique projectile motion.
- Horizontal projectile motion.
Oblique Projectile
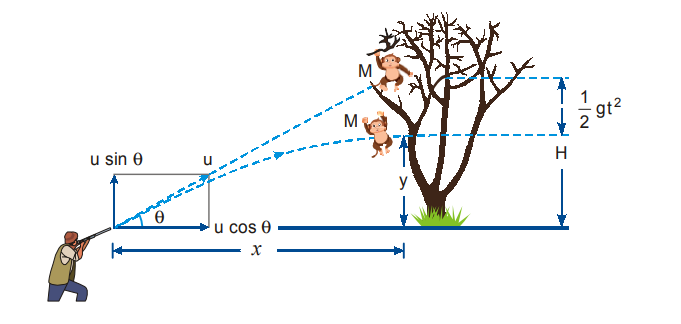
When a body is thrown at an angle from horizontal then motion under gravity is known as oblique projectile motion.
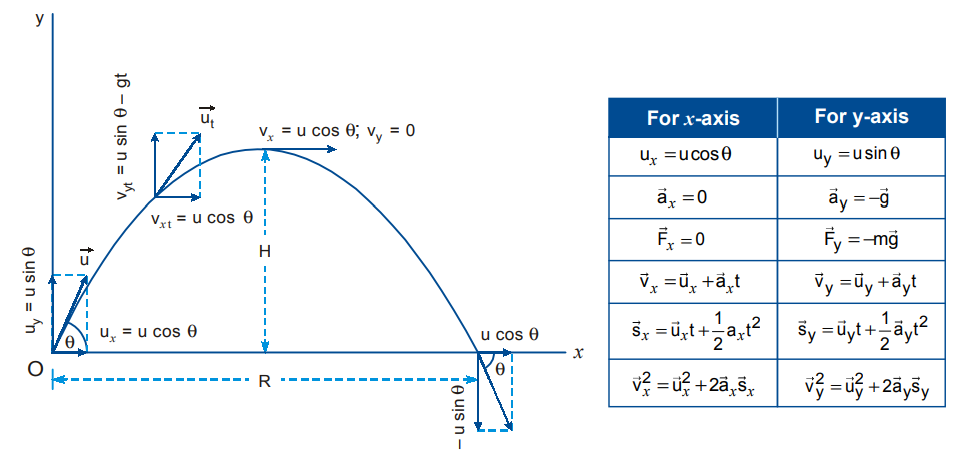
Equation of trajectory : A projectile thrown with velocity u at an angle θ with the horizontal. The velocity u can be resolved into two rectangular components.
u cosθ component along X-axis and u sin θ component along Y-axis.
For horizontal motion,
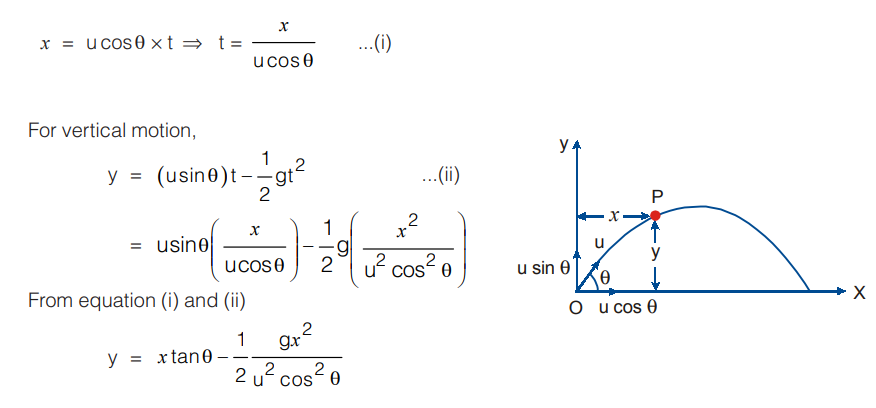
This equation shows that the trajectory of projectile is parabolic because it is similar to equation of parabola
y=ax – bx2
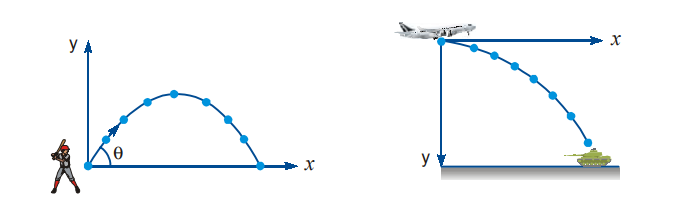
Horizontal Projectile
Trajectory of horizontal projectile: The horizontal displacement x is governed by the equation
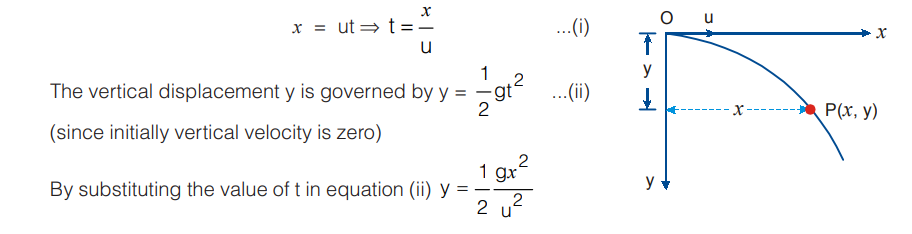
Relative Motion In Two Dimensions

Motion of Man while Crossing a River
Consider a man swimming in a river with a velocity of V→MR relative to river at an angle of θ with the river flow. The velocity of river is V→R. Let there be two observers I and II.
Observer I is on ground.
Observer II is on a raft floating along with the river and hence moving with the same velocity as that of river.
Hence motion w.r.t. observer II is same as motion w.r.t. river. i.e., the man will appear to swim at an angle θ with the river flow for observer II.
For observer I the velocity of swimmer will be V→M = V→MR + V→R
Hence the swimmer will appear to move at an angle θ′ with the river flow.
- Motion of swimmer for observer I
- Motion of swimmer for observer II
The motion observed by the observer I is same as the motion with respect to the ground frame of reference.
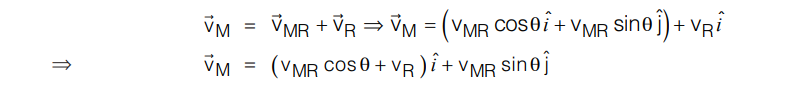
Here vMR sinθ is the component of velocity of man in the direction perpendicular to the river flow. This component of velocity is responsible for the man crossing the river. Hence if the time to cross the river is t,
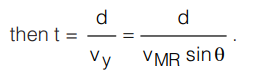
Drift
It is defined as the displacement of man in the direction of river flow. It is simply the displacement along x-axis, during the period the man crosses the river.
(vMR cos θ + vR) is the component of velocity of man in the direction of river flow and this component of velocity is responsible for drift along the river flow. If drift is x then,
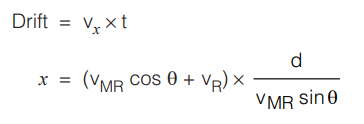
Crossing the River in Shortest Time

NOTE: In the case of crossing the river in shortest time there will be drift along x direction.
Crossing the River in Shortest Path, Minimum Drift
The minimum possible drift is zero. In this case the man swims in the direction perpendicular to the river flow as seen from the ground. This path is known as Shortest Path.

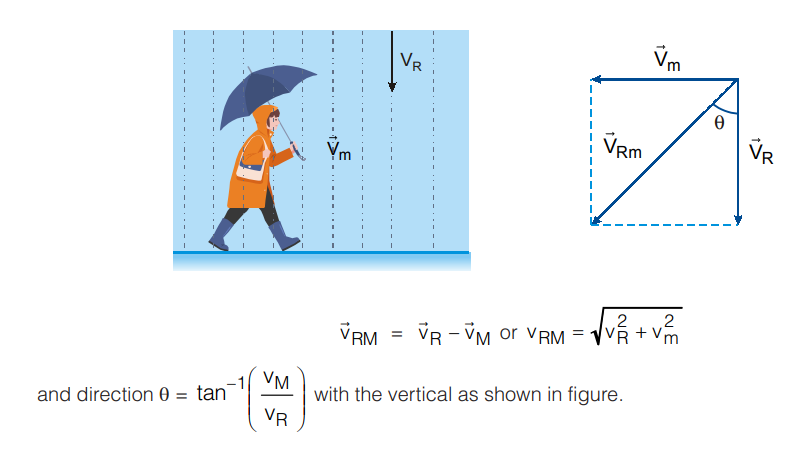
Rain Main Problems
If rain is falling vertically with a velocity V→R and an observer is moving horizontally with velocity V→M, the velocity of rain to relative observer will be:
Circular Motion
Angular Displacement (dθ or θ)
The angle described by radius vector is called angular displacement. Infinitesimal angular displacement is a vector quantity. However, finite angular displacement is
S.I. Unit : Radian
Dimension : M°L°T°

Angular Velocity (ω)
The rate of change of angular displacement with time is called angular velocity. It is a vector quantity. The angle traced per unit time by the radius vector is called angular speed.
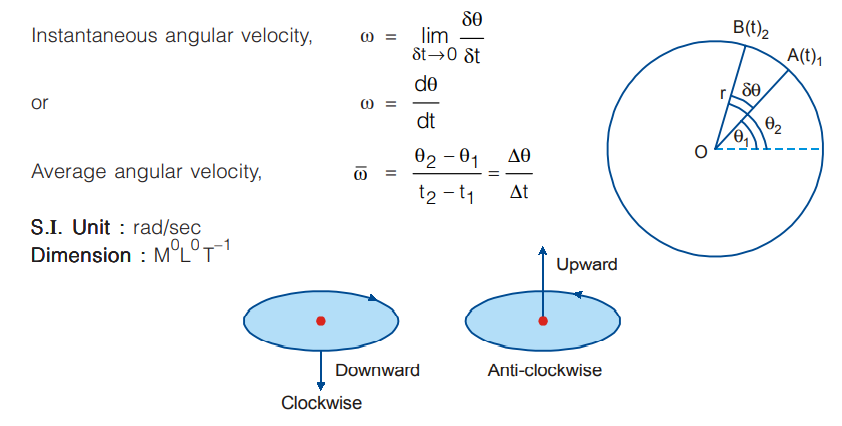
- Direction : Infinitesimal angular displacement, angular velocity and angular acceleration are vector quantities whose direction is given by right hand rule.
Relation Between Angular Velocity and Linear Velocity
Suppose the particle moves along a circular path from point A to point B in infinitesimally time dt.

Linear velocity of a particle performing circular motion is the vector product of its angular velocity and radius vector.
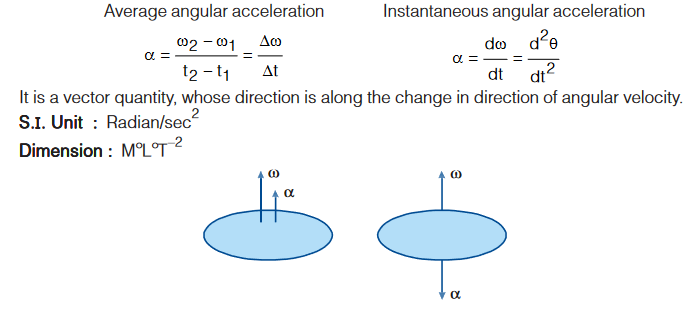
Angular Acceleration (α)
The rate of change of angular velocity with time is called angular acceleration.
Relation Between Angular Acceleration and Linear Acceleration
For perfect circular motion we know v = ωr
On differentiating with respect to time
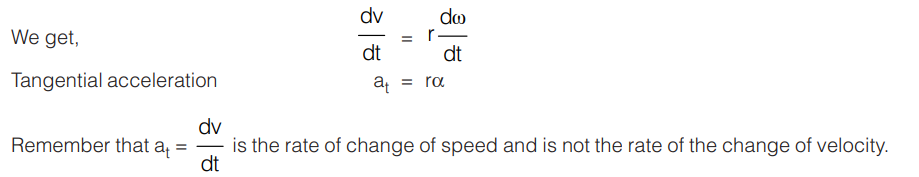
It is, therefore not equal to the net acceleration.
Infact it is the component of acceleration along the tangent and hence suffix t is used for tangential acceleration.
at is known as the tangential acceleration.
![]()