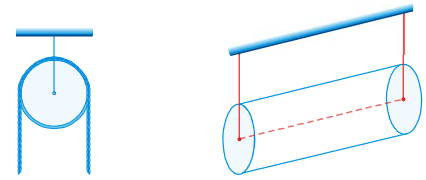
Pulley Block System
Single Fixed Pulley
It is a wheel like structure, generally disc or cylinder used for producing desired direction of motion.
Assumption for ideal pulley– It is smooth (frictionless) and massless.
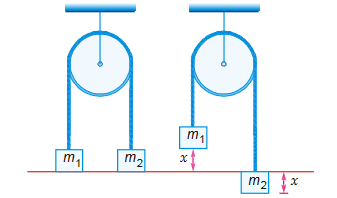
If the pulley is fixed and two ends of the rope are free to move.
If the mass m2 goes down by a distance x, then the mass m1 will rise upward by the same distance.
Hence velocity, v = dx / dt is same in magnitude for both blocks, but their directions are opposite
and acceleration a = dv / dt is same in magnitude for both blocks, but opposite in directions.
Kinematic constraints are equations that relate the motion of two or more bodies. By differentiating the kinematic constraints for the position of the particle in a system, the corresponding kinematic constraints among the velocities and accelerations of the particles may be obtained.
Example :
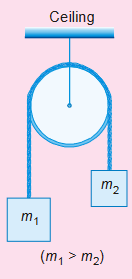
Two blocks of masses m1 and m2 are connected to each other by a light, inextensible string that passes over a light, smooth pulley fixed to the ceiling (see figure). Find the acceleration of each block and the force exerted on the ceiling, by the arrangement.
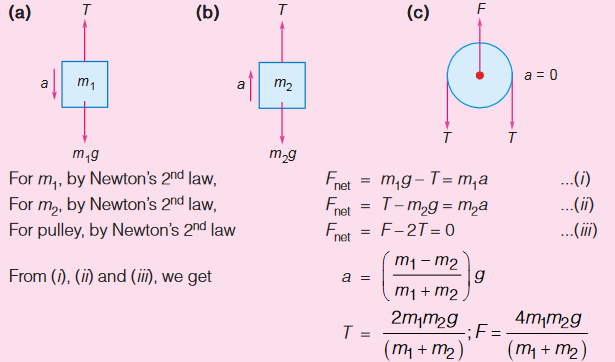
If m1 goes down by a distance x, m2 moves up by a distance x. If the acceleration of m1 is a downwards, the acceleration of m2 is a upwards. As the string is light and pulley is smooth, the tensions in the two parts of the string are equal, Let it be T. Now draw the free body diagram of the blocks and the pulley.
Example :
A light rope is passed over a pulley such that at its one end a block is attached, and on the other end a boy is climbing up with acceleration g/2 relative to rope. Mass of the block is 30 kg and that of the boy is 40 kg. Find the tension and acceleration of the rope.
Example :
Two blocks of masses m1 and m2 are connected by a light inextensible string and pulled up by external force F on inclined plane having inclination angle θ. Then find acceleration of block and tension in the string.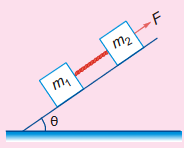
Solution :
Single Movable Pulley with one end fixed
One end of the string passing over the pulley is fixed while the pulley and other end is free to move.
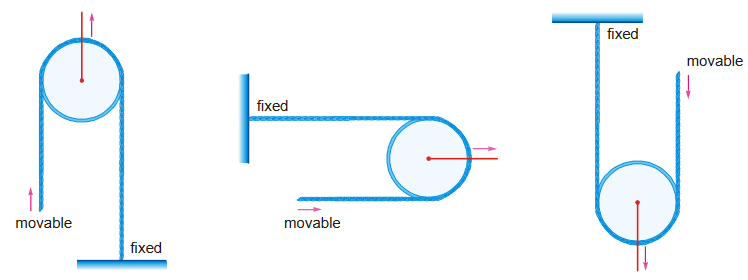
To get the relation between two velocities or acceleration, let us assume that initially both ends are parallel and free.
If we move the pulley by a distance x upward, then both ends of string also move by a distance x upward. Now shift one end to original position and fix it on ground. The other end will move further by a distance x upward as explained in diagram. (so we will observe that free end moved by 2x)
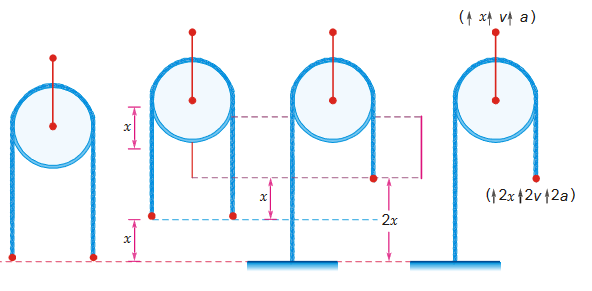
Conclusion : If the pulley moves a distance x then the free end of string moves a distance 2x. Or, if free end of the string moves a distance x then pulley will move a distance x/2. In figure shows the masses are attached to the inextensible string.
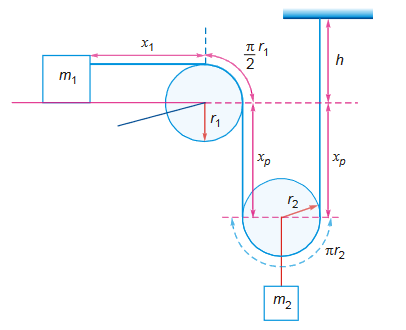
Method : 2
As one end of the movable pulley is fixed if the pulley moves with acceleration a2 downwards other end moves with acceleration 2 a2 downwards.
Thus, a1 = 2a2
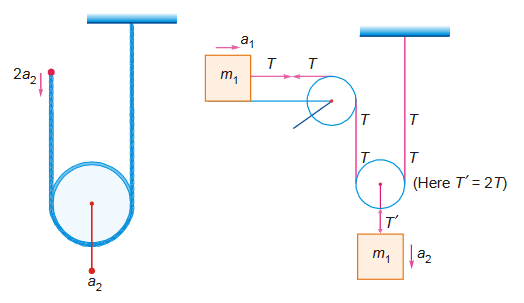
Single Movable Pulley with all ends free to move
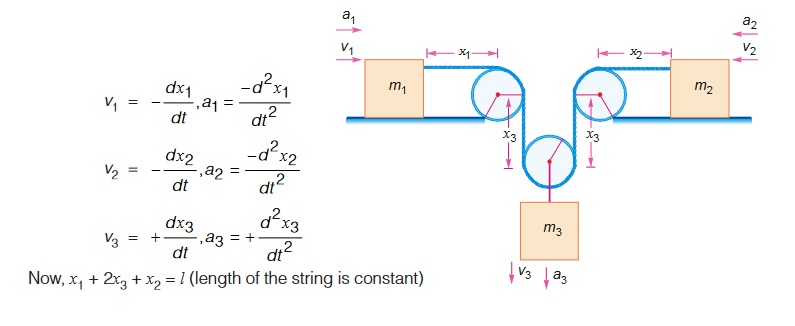
Combination of Fixed and Movable Pulley
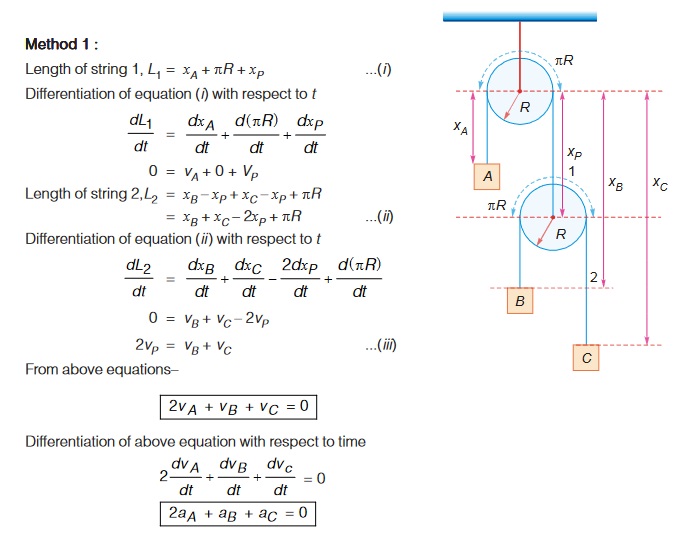
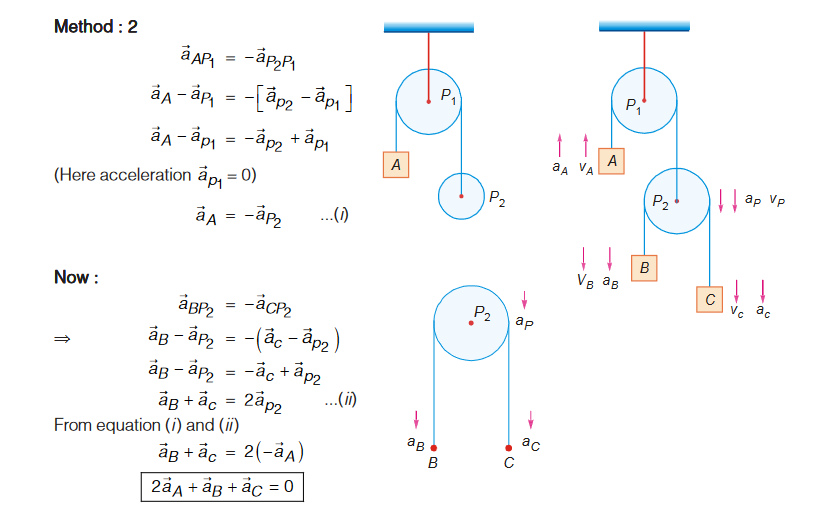
Example :
Figure shows an arrangement of a pulley-mass system. Find a relation between the accelerations of the two blocks. Also find their values.
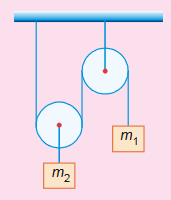
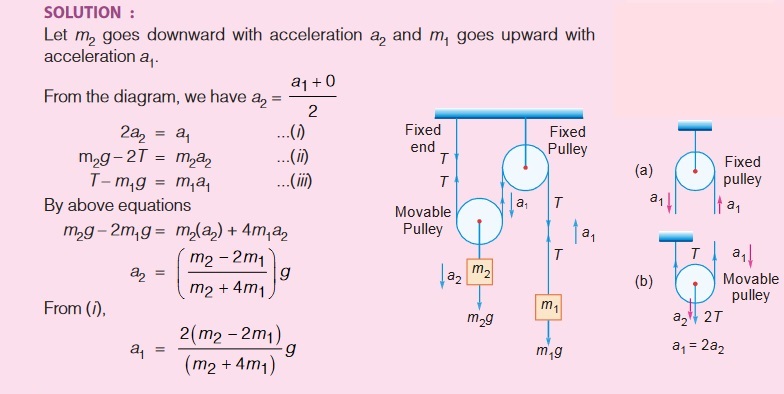NOTE : For movable pulley, downward force is 2T. This is so because the pulley is light and the net force on it must be zero.
Classroom Courses
