Relative Motion in River Flow
If a man can swim relative to water with velocity V→mR and water is flowing relative to ground with velocity V→R, velocity of man relative to ground V→m will be given by :

Downstream & Upstream Swimming
Velocity of river is u and velocity of man in still water is v.


Example :
A swimmer capable of swimming with velocity ‘v’ relative to water jumps in a flowing river having velocity ‘u’. The man swims a distance d down stream and returns back to the original position. Find out the time taken in complete motion.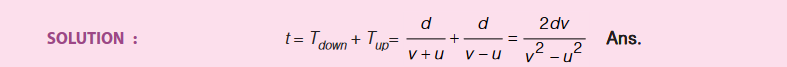
Motion of Man while crossing a river
Consider a man swimming in a river with a velocity of V→MR relative to river at an angle of θ with the river flow. The velocity of river is V→R . Let there be two observers I and II.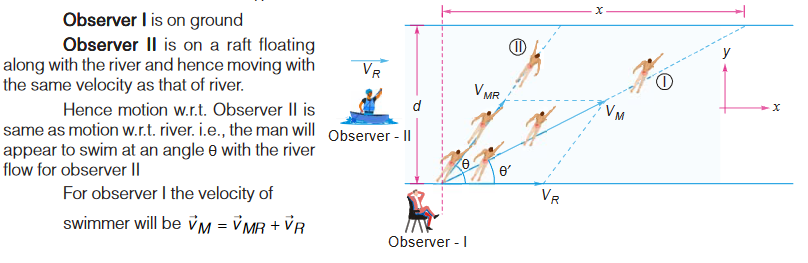
Hence the swimmer will appear to move at an angle θ’ with the river flow.
- Motion of swimmer for observer I
- Motion of swimmer for observer II
The motion observed by the observer I is same as the motion with respect to the ground frame of reference.
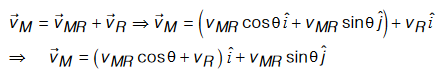
Here vMR sinθ is the component of velocity of man in the direction perpendicular to the river flow. This component of velocity is responsible for the man crossing the river. Hence if the time to cross the river is t,
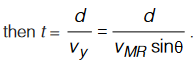
Drift
It is defined as the displacement of man in the direction of river flow. It is simply the displacement along x-axis, during the period the man crosses the river. (vMR cos θ + vR) is the component of velocity of man in the direction of river flow and this component of velocity is responsible for drift along the river flow. If drift is x then,
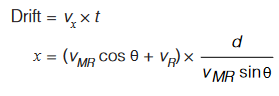
Crossing the river in shortest time

Note:
In the case of crossing the river in shortest time there will be drift along x direction.Crossing the river in shortest path, Minimum Drift
The minimum possible drift is zero. In this case the man swims in the direction perpendicular to the river flow as seen from the ground. This path is known as shortest path
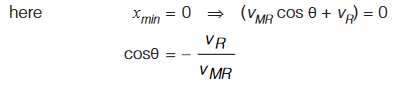

Example :
A 400 m wide river is flowing at a rate of 2.0 m/s. A boat is sailing with a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. (a) Find the time taken by the boat to reach the opposite bank. (b) How far from the point directly opposite to the starting point does the boat reach the opposite bank? (c) In what direction does the boat actually move, with river flow (downstream).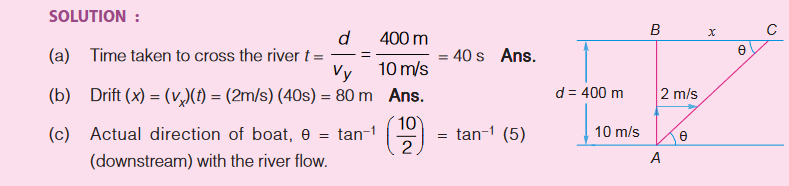
Example :
A man can swim at the rate of 5 km/h in still water. A 1 km wide river flows at the rate of 3 km/h The man wishes to swim across the river directly opposite to the starting point. (a) Along what direction must the man swim? (b) What should be his resultant velocity? (c) How much time will he take to cross the river?
Example :
A river is following from west to east at a speed of 5 metres/minute. A boy on the south bank of river, capable of swimming at 10 metres/minute in still water, wants to swim across the river in the shortest time, (i) Find the direction in which he should swim, (ii) Find the direction when drift along the river is zero.