Solutions

Vapour Pressure

When a liquid is placed in a closed container, it evaporates and converts to vapour. After some time, the liquid and the vapour reach equilibrium, i.e., the rate of evaporation becomes equal to the rate of condensation. At this point of time, the pressure exerted by the vapours of the liquid on the surface of the liquid and on the walls of the container is called the vapour pressure of the liquid.

Does the vapour pressure of a liquid depend on the volume of the vessel, shape of the vessel or the amount of liquid taken in the container?

These questions can be answered by invoking the concept of equilibrium constant. For the equilibrium, ⇆ liquid vapour, the K_p for the equilibrium would be = P_vap, since this is the pressure exerted by the vapours at equilibrium (by definition). We know K_p depends only on temperature and the nature of substance. This means that vapour pressure of a liquid will also be constant at a given temperature and will depend on temperature and the nature of liquid.

Therefore, it should be noted that whatever be the volume or shape of the vessel, or the amount of liquid in it (assuming it to be more than the minimum amount required), the vapour pressure of a liquid is constant at a given temperature and changes only with the change of temperature of the liquid.

Moreover, on addition of any substance to the liquid, as long as the substance does not dissolve in the liquid and completely covers the surface, the vapour pressure of a liquid remains constant.

SECTION 3 : RAOULT’S LAW

For a solution of two miscible liquids, the partial vapour pressure of each liquid is less than the respective vapour pressure of the pure liquid because of the decrease in surface area of the liquid from which fewer molecules go into vapour phase. Raoult’s law states that the partial vapour pressure of a liquid is directly proportional to its mole fraction in solution.

where P_A is the partial vapour pressure of the liquid and X_A is its mole fraction in solution. We can determine the value of the proportionality constant as follows.

For pure solvent, the value of mole fraction is unity, i.e., X_A = 1 and the vapour pressure is equal to the vapour pressure of the pure solvent

Partial vapour pressure of the liquid = Vapour pressure of the pure liquid in the solution × Mole fraction of the liquid in solution.

3.1 RAOULT’S LAW FOR A SOLUTION CONTAINING A VOLATILE SOLUTE

Raoult’s law states that the partial vapour pressure of a component of a solution of two miscible liquids A and B at a given temperature is equal to the product of the vapour pressure of the pure component at that temperature and its mole fraction in the solution.

Mathematical Expression: Let us assume that a solution has n_A moles of liquid A and n_B moles of liquid B. Let be the vapour pressure of the pure liquid A and is the vapour pressure of the pure liquid B.

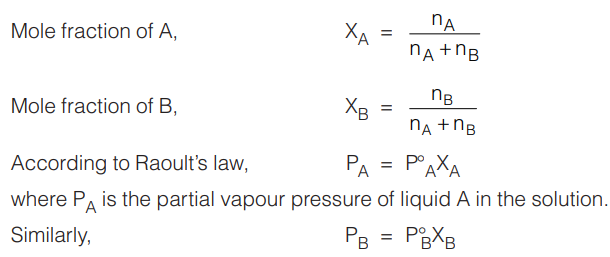
where P_B is the partial vapour pressure of liquid B in the solution.

The total vapour pressure of an ideal solution containing components A and B is the sum of partial vapour pressures of all the components (Dalton’s law of partial pressures)

3.2 RAOULT’S LAW & DALTON’S LAW

Further, by assuming ideal behavior of vapour phase of both components we also can determine vapour phase composition above the surface of solution of equilibrium.

If x’_A and x’_B are the mole-fractions of gas-phase components A and B, then by the applying Dalton’s Law of partial pressure

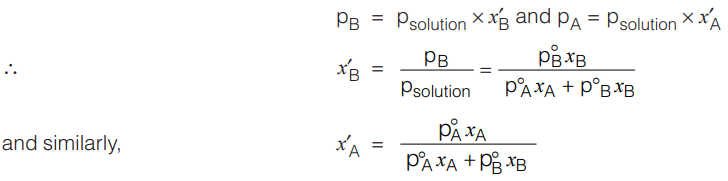
Now, if the vapour phase is condensed, we get the distillate. Therefore, composition of distillate will remain same as vapour phase composition.

In terms of number of moles, it also can be represented as

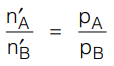
where n‘_A and n‘_B are number of moles of component A and B in distilled water (Vapour-phase composition).

In terms of mass-ratio we can transform the above relation as:

where w and M are representing mass in grams and molar-masses for respective components.

These formulae are applicable when vapour phase is in equilibrium with the solution and distilled mass here is of the same vapours collected over a solution.

SECTION 4 : IDEAL AND NON-IDEAL SOLUTIONS

4.1 IDEAL SOLUTIONS

A solution can be termed as ideal, if it falls into any one of the given below categories:

1. Raoult’s Law : An ideal solution is that solution in which each component obeys Raoult’s law under all conditions of temperature and This law is described in the earlier section.
2. Thermodynamics : An ideal solution is defined as the one in which no volume change and enthalpy change takes place on mixing the solute and the solvent in any proportion, i.e., ∆V_mixing = 0 and ∆H_mixing = 0.
3. Molecular Interactions: An ideal solution is defined as the solution in which the intermolecular interactions between the components are of the same magnitude as the intermolecular attractions found in the pure components.

In actual practice, no solution is ideal. However, when concentration of solute is very low the solution behaves ideally. Therefore, very dilute solutions can be considered to be almost ideal in behavior.

In general, substances possessing similar structure and polarities form nearly ideal solution. For example,

1. Benzene + Toluene
2. Hexane + Heptane
3. Ethyl bromide + Ethyl Iodide
4. Chlorobenzene + Bromobenzene

The graphical behavior of ideal solutions has been shown here.

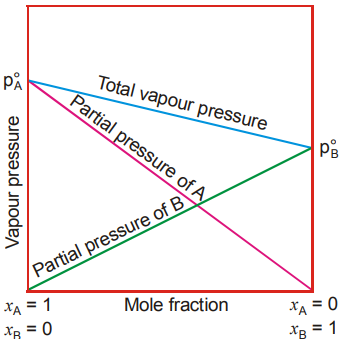
4.2 NON-IDEAL SOLUTIONS

A non-ideal solution is defined as the one which does not obey Raoult’s law. These are divided into two types as explained below :

Non-Ideal Solutions showing Positive Deviations

These can be defined on the basis of :

1. Molecular interactions : A non-ideal solution showing positive deviation is defined as the one in which the intermolecular forces of interactions between the molecules are weaker as the interactions found in any one of the pure components or both.
2. Thermodynamics : A non-ideal solution is defined as the one in which there is a slight increase in volume on mixing and absorption of heat takes place on mixing DV_mixing > 0, DH_mixing > 0. Some examples are:
   1. Acetone + carbon disulphide
   2. Acetone + ethyl alcohol
   3. Acetone + benzene
   4. Carbon tetrachloride + Chloroform
   5. Methyl alcohol + water
   6. Ethyl alcohol + water

In the given examples from (i) to (vi), the molecules possessing weaker interactions get in between the molecules possessing stronger interactions thereby reducing them. In examples (v) and (vi), though both the components have hydrogen bonding but the extent of hydrogen bonding in the case of water is more than that in the case of alcohols.

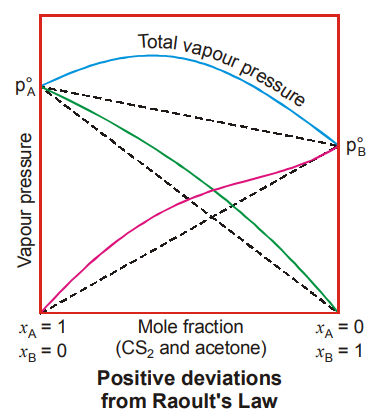
Graphical Representation

For one intermediate composition, the total vapour pressure of such a solution will be the highest and the boiling point will be the lowest. This solution acquires the property of boiling at a constant temperature and its composition remains unchanged. Liquid mixtures, which boil out without any change in the composition are called azeotropes or azeotropic mixtures. In case of positive deviations, we get minimum boiling azeotropes. The topic on azeotropes is discussed in the forthcoming section.

Non-Ideal Solutions showing Negative Deviations

These can be defined on the basis of :

1. Molecular Interactions: Solutions in which forces of interactions between the components is more than that in between the pure components are the ones showing negative deviation from Raoult’s law.
2. Thermodynamics: In the case of such solutions, a slight decrease in volume and evolution of heat takes place on mixing, i.e., ∆V_mixing < 0 and ∆H_mixing < 0.

Examples :

(i)   Chloroform + Acetone            (ii)   Acetone + Aniline             (iii) Acetic acid + Pyridine

(iv) HCl + water                           (v) HNO₃ + water

In the above examples from (i) to (iii), the weak interactions are being replaced by strong hydrogen bonds, thus reducing the escaping tendency of the molecules. In case of (iii), one of the constituents are basic while the other is acidic. Whereas (iv) and (v) involve an aqueous solution of a strong volatile acid such as a halogen acid. In these cases, non-volatile ions are formed as a result of interaction of ions of the acid with water.

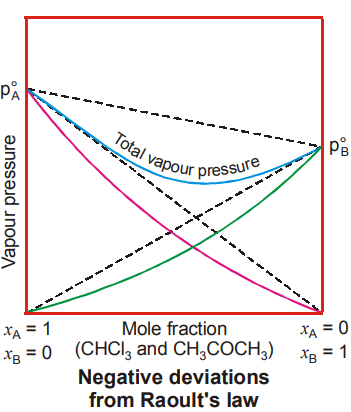
Graphical Representation

For such solutions, at one intermediate composition, the total pressure exhibited by the components is the least and hence the boiling point of the liquid mixture at that composition would be highest. The solution will thus distil without a change in composition and provide an example of maximum boiling azeotrope.

7.1 RELATIVE LOWERING OF VAPOUR PRESSURE

According to Raoult’s law, the lowering of vapour pressure of a solvent is given by

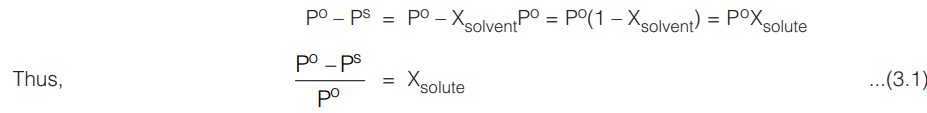
The expression (P^o – P_S) /P^o is known as the relative lowering of vapour pressure and according to Eqn. (3.1), this is equal to the mole fraction of the solute in the solution.

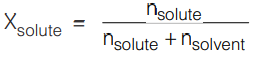
It can be seen that X_solute is not directly proportional to the number of moles of solute. So, it may be seen that the relative lowering of vapour pressure would not qualify as a colligative property. But since these properties are shown by ideal solutions which happen to be infinitely dilute, it can be assumed n_solute << n_solvent, therefore, in the denominator, n_solute can be ignored in comparison to n_solvent.

7.2 ELEVATION OF BOILING POINT

Boiling is the phenomenon in which a liquid converts to the vapor state from any part of the liquid. Evaporation on the other hand is the conversion of a liquid into the vapour from the surface of the liquid.

At a temperature below the boiling point of the liquid, liquid molecules from the bulk of the liquid cannot form vapour bubble and escape. This is because the pressure inside the vapour bubble is the vapour pressure of the liquid at that temperature and as long as the vapour pressure is less than the atmospheric pressure, the bubble cannot be formed. This is due to the fact that the downward pressure of the atmosphere is more than the internal outward pressure inside the vapour bubble.

When the vapour pressure becomes slightly greater than the internal pressure, the vapours can form from any part of the liquid and escape. So, the limiting pressure is the atmospheric pressure. Therefore, a liquid boils at a temperature when its vapour pressure becomes equal to the atmospheric pressure.

Since the addition of a non-volatile solute decreases the vapour pressure of the solvent, the boiling point of the solution becomes greater than that of the pure solvent. This can be understood from the figure shown here.

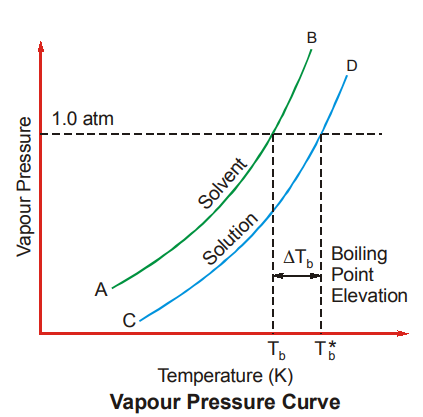
If T_b is the boiling point of pure solvent and T_b* is the boiling point of the solution, then the elevation in boiling point is represented as ∆T_b.

Thus,

T_b* – T_b = ∆T_b

Since, elevation in boiling point is proportional to the decrease in vapour pressure which in turn is proportional to concentration of solute. Thus,

∆T_b ∝ m

where m is the molality of the solution.

or

∆T_b ∝ K_bm

where K_b is the molal boiling point elevation constant or ebullioscopic constant.

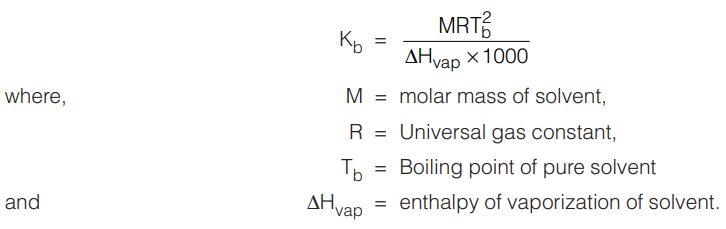
Molal Boiling Point Elevation Constant (K_b)

It is the elevation in boiling point achieved when a solution of a non-volatile solute of concentration 1 molal is boiled. Its units are K kg mol^–1. K_b is related to molar enthalpy of vaporization as

7.3 DEPRESSION IN FREEZING POINT

Freezing is the phenomena when a liquid is in equilibrium with its solid phase. At the freezing temperature, both the liquid as well as the solid is in equilibrium with the vapours. This implies that the vapour pressure of both the liquid and the solid are same at the freezing point. Therefore, alternatively freezing point can be defined as the temperature when the vapour pressure of the liquid and the solid are equal.

On adding a non-volatile solute, the freezing point of the solution decreases compared to that of the pure liquid because the solid that separates out from both is assumed to be pure (this means that when a solution is frozen only the liquid freezes out leaving behind the solute). This can be understood from the figure.

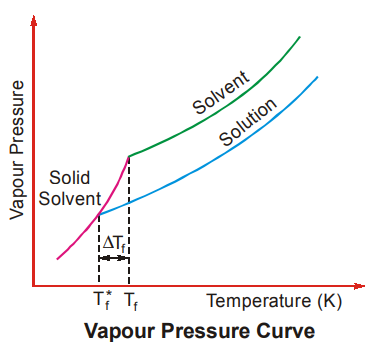
If T_f is the freezing point of pure solvent and T_f* is the freezing point of the solution, then the depression in freezing point is represented as ∆T_f.

Thus,

T_f* – T_f = ∆T_f

Since depression in freezing point is proportional to the decrease in vapour pressure which in turn is proportional to the concentration of solute. Thus,

∆T_f ∝ m

where m is the molality of the solution. or

∆T_f ∝ K_fm

where K_f is the molal freezing point depression constant or cryoscopic constant.

Molal Freezing Point Depression Constant (K_f)

It is the depression in freezing point achieved when a solution of a non-volatile solute of concentration 1 molal is frozen. Its units are K kg mol^–1.

K_f is related to the molar enthalpy of fusion as :

7.4 OSMOTIC PRESSURE

Osmosis is defined as the spontaneous flow of solvent into solution or from a more dilute to a more concentrated solution, when the two solutions are separated by a suitable membrane. The membrane allows the free passage of the solvent but not of the dissolved substances. Membranes possessing this property are said to be semipermeable.

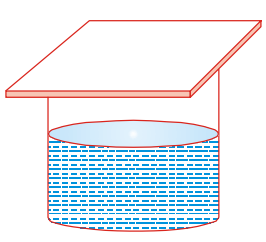
The phenomenon of osmosis may be illustrated in a simple manner by tying an animal membrane, over the end of an inverted thistle tube, which is then partly filled with a concentrated solution of sucrose (cane sugar) and dipped into a beaker of water, as shown in the given figure. The level of the liquid will rise in the tube until the hydrostatic pressure so produced is sufficient to stop the flow of water. It is seen, therefore, that as a result of osmosis, a pressure is developed which opposes the tendency for the solvent to pass through the semipermeable membrane into the solution. This pressure is called the osmotic pressure of the solution. It is defined as “the excess pressure that must be applied to a solution to prevent the passage into of solvent when the two liquids are separated by a perfectly semipermeable membrane”.

There has been some tendency to think of osmotic pressure as a pressure produced by the solution, but this point of view is misleading. The osmotic pressure is brought into existence only when the solution is separated from the solvent by a semipermeable membrane. The resulting osmosis or tendency for osmosis to occur then produces an excess pressure in the solution. When this excess pressure attains the value of the osmotic pressure, the tendency for solvent to enter the solution is exactly counterbalanced by the reverse tendency and a condition of equilibrium results.

For the accurate measurement of osmotic pressure, it is necessary to have a membrane that is perfectly semipermeable. Artificial membranes made of copper ferrocyanide, Cu₂Fe(CN)₆, is the best material for osmosis.

The osmotic pressure of a dilute solution of a non-volatile solute is given by

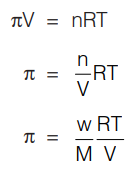
where π is the osmotic pressure in atmospheres, n = number of moles of solute (W/M) in V litres of solution at temperature T (Kelvin), R = 0.0821 Lit atm K^–1 mol^–1. C is the molarity of the solution. Measurement of osmotic pressure provides a method of determining molecular weights of proteins, polymer and other macromolecules.

SECTION 8 : VANT HOFF FACTOR (i)

Since colligative properties depend on the number of particles of the solute, in some cases where the solute associates or dissociates in solution, abnormal results for colligative properties are obtained.

Dissociation: Let us consider the case of acetic acid dissolved in water. Let the number of mole of acetic acid dissolved be ‘n’.

CH₃COOH ⇆ CH₃COO^– + H⁺

Initial no. of mole                                n                      0                0

After dissociation                                n(1 – α)          nα             nα

Total moles of solute =                      n(1 + α)

Theoretical colligative property (for example ∆T_b) (based on the number of mole of CH₃COOH added)

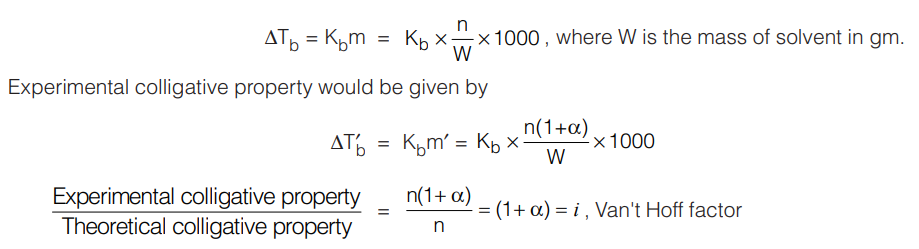
Association: Let us consider the case of acetic acid dissolved in benzene. Let the number of mole of acetic acid dissolved be ‘n’ and it forms dimmer in benzene.

2CH₃COOH  ⇆  (CH₃COOH)₂

Initial no. of mole                                 n                       0

After dissociation                                 n(1 – α)             nα/2

Total moles of solute =                       n(1 – α/2)

Theoretical colligative property (for example ∆T_b) (based on the number of mole of CH₃COOH added)

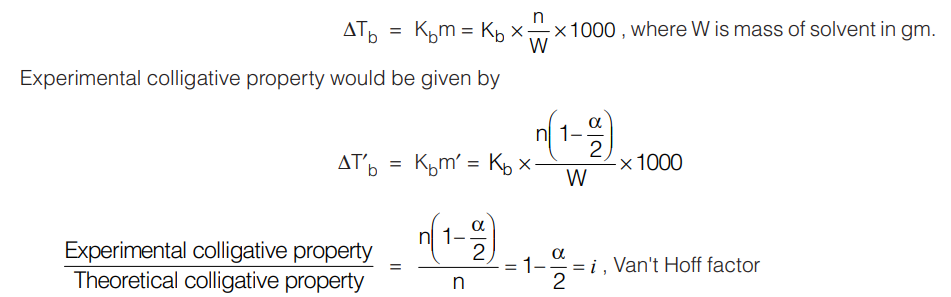
Therefore, for dissociation i >1 and for association i < 1. When a solute neither dissociates nor associates, the Van’t Hoff factor is equal to 1.