Structure of Atom

SECTION 1 : CONSTITUENTS OF AN ATOM

As discussed above, the ultimate particle of matter is not the atom. As we know today, an atom consists of subatomic particles, the electron, proton and the neutron. In chronology, the discovery of the fundamental particles of the atom was done through a series of experiements. Some of these great developments have been highlighted here.

1.1 CATHODE RAY DISCHARGE TUBE

(MICHAEL FARADAY, 1850)

Experiment was done to analyze the discharge of electricity through gases at very low pressure. An observable electrical discharge was noticed when very high potential difference of around 1 kV was applied. Radiation was seen emanating from the Cathode (negative plate) towards the Anode (positive plate).

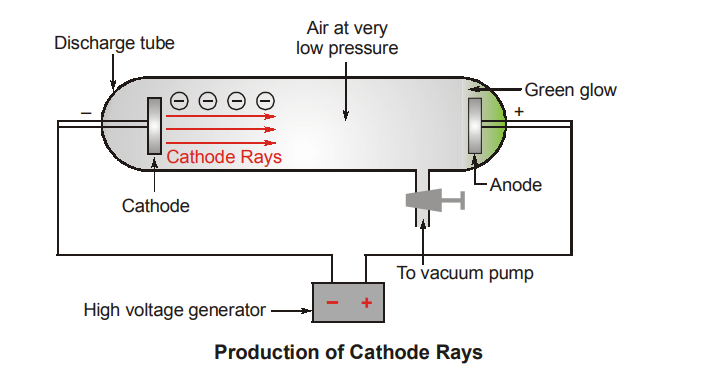
The Cathode ray tube is a thin glass tube which has two metal plate electrodes sealed within it (Refer to above figure). Once this high voltage is applied current starts flowing through a stream of particles from the cathode to the anode.

The anode was then perforated and the beam of cathode rays allowed to strike a phosphorescent material such as Zinc Sulphide. When these rays strike Zinc Sulphide a bright spot is produced on its surface.

The conclusions of the Cathode Ray Tube Experiment include :

1. Cathode rays travel in straight lines but are deflected towards the positive plate of an externally applied electric field.
2. These rays are invisible, however they can be detected by use of phosphorescent materials, which glow when these rays strike them.
3. Their nature does not depend on the nature of gas taken in the tube and on the material of which the cathode is made.

1.2 J.J. THOMSON’S CHARGE TO MASS RATIO EXPERIMENT

field and a mutually perpendicular magnetic field over a fast moving cathode ray beam.

In the presence of these fields the particles of cathode ray deflect. However, the field strengths are adjusted in such a way that the cathode rays followed a non-deflecting path.

From this experiment, the specific charge or charge to mass ratio of the electron was estimated to be 1.7588 × 10⁸ C/g or 1.7588 × 10¹¹ C/kg.

It was found that the e/m of an electron is independent of the gas in independent of the gas the discharge tube and metal used as the electr used as the electrode.

1.3 ROBERT A MILLIKEN’S OIL DROP EXPERIMENT

Milliken was able to determine the charge on the electron through this experiment. An electrical condenser with two plates was assembled.

The air in the chamber was ionized using X-Rays. Now, fine spray of oil droplets were made to enter through the upper plate.

Rate of fall of these droplets was used as a measure to establish the charge on them.

Milliken inferred that the charge acquired by these droplets was quantized and an integral multiple of a fundamental charge value.

He estimated the charge on the electron to be –1.6 × 10^–19 Coulombs. However, the accepted value today is –1.6022 × 10^–19 Coulombs.

Finally, the mass of the electron was estimated by using the J. J. Thomson’s calculated charge to mass ratio value as :

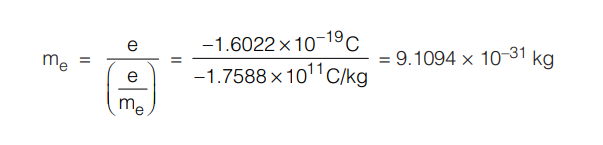
SECTION 2 : NUCLEAR MODEL OF THE ATOM

2.2 MODEL-2 : THE RUTHERFORD MODEL

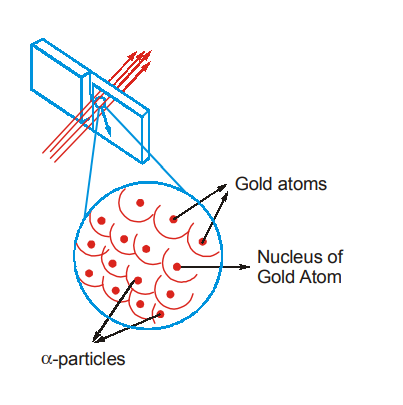
In 1908, the plum pudding model was overthrown by a simple experiment. The New Zealander Ernest Rutherford asked two students (Hans Geiger and Ernest Marsden) to shoot α-particles (he knew that some element like Radon emit positively charged particles, which he called alpha (α) particles) toward a piece of gold foil only a few atoms thick. If atoms were indeed like blobs of positively charged jelly, then all the α-particles would leave similar paths as they move through the foil.

From the experiment, Rutherford made the following observations:

1. Almost all the α-particles did pass through the gold foil undeflected.
2. Some of these particles were deflected by small angles; about 1 in 20,000 was deflected through more than 90°.
3. A few α-particles bounced straight back in the direction from which they had came. “It was almost incredible,” said Rutherford, “as if you had fired a 15-inch shell at a piece of tissue paper and it came back and hit you”.

Conclusions from the above observations:

1. Atoms had to contain massive point like centers of positively charge surrounded by a large volume of mostly empty space. Rutherford called the point of positively charged region, the nucleus.
2. He reasoned that closer the path of the α-particles to the nucleus of the atom, greater the deflection it experiences and the a-particles which directly hit on the molecules would rebound back.
3. The electrons are thinly distributed throughout the space around the nucleus. If the nucleus in a hydrogen atom were the size of a fly at the center of a cricket stadium, then the space occupied by the electron would be about the size of the entire cricket stadium.

SECTION 3 : NATURE OF LIGHT AND ELECTROMAGNETIC SPECTRA

In this section, we will study the nature of electromagnetic radiations, the spectrum obtained from light and the quantum theory of radiation which entirely changed our view of understanding light and its behaviour.

3.1 ELECTROMAGNETIC RADIATIONS

Ordinary light, X-rays, γ-rays, etc. are called electromagnetic radiations and they have wave characteristics. These radiations are called electromagnetic radiations because when they pass through a point in space, they produce oscillating electric and magnetic fields at that point. These waves propagate in free space (vacuum) with the velocity of light.

There are some fundamental characteristics associated with wave motion. These are discussed here in some detail:

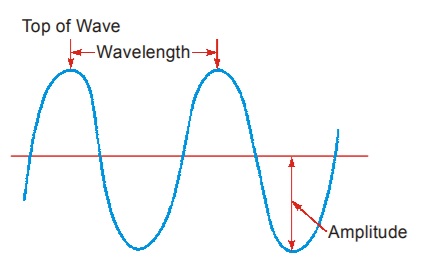
(i) Wavelength (λ) : Consider a wave profile as shown in figure. The distance between two successive cr successive crests or tr ests or troughs is known as wavelength ( wavelength (λ). It is measured in cm or ) Angstrom unit (Å) or any other unit of length. For our knowledge, we must know that 1 Å = 10–8 cm = 10–10 m Sometimes, nanometre (nm) = 10–9 m is used to express wavelength.

(ii) Frequency (ν) : The number of waves that pass through a given point in one second is called its frequency (number of waves per second). Frequency (ν) is expressed in cycles per second (cps) or hertz (Hz).

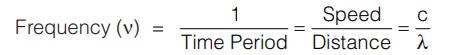
(iii) Velocity (c) : The distance travelled by a wave in 1 second is its velocity ‘c’. This means, Velocity = Frequency × Wavelength i.e.,

c = ν × λ

The velocity c of all types of electromagnetic radiation is established experimentally to be a constant, in vacuum and equal to 3 × 10¹⁰ cm/s or 3 × 10⁸ ms^–1 (about 186000 miles/s). This is the velocity of light.

(iv) Amplitude (A) : The height of a crest (or) depth of a trough is representative of the Amplitude of the wave. The amplitude gives us information about the intensity (brightness) of an electromagnetic wave.

(v) Wave Number ( ν ) : The number of waves present per unit length is the wave number of a wave. Among EM Waves this is calculated as the reciprocal of wavelength.

3.3 PLANCK’S QUANTUM THEORY

According to this theory, a body cannot emit or absorb energy in the form of radiation continuously; energy can be taken up or given out as whole number multiples of a definite amount known as a quantum (or packet). Light is imagined to consist of a stream of particles called photons. If E is the energy of a photon, its quantum for a particular radiation of frequency ν second^–1 is given by quantum theory as E = hν where ‘h’ is a universal constant known as Planck’s constant; h = 6.626 × 10^–27 erg-sec or 6.626 × 10^–34 Joule- second (J-s).

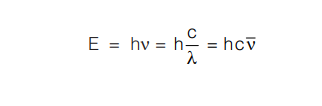
According to quantum theory, a body can emit or absorb either 1 quantum of energy (hν) or whole number of multiples of this unit, 2hν, 3hν, 4hν, ….. nhν.

SECTION 4 : BOHR’S MODEL OF HYDROGEN ATOM

In order to account for the permanence of the atom and to explain the spectrum of atomic hydrogen, Bohr enunciated a master theory. Bohr retained the Rutherford model of a central positively charged nucleus containing practically all the mass surrounded by a planetary system of electrons whose number is equal to the nuclear charge. He made use of Planck’s quantum theory and gave the following postulates : The postulates are well defined for the Hydrogen atom and some other single electron species that are similar to hydrogen such as He⁺, Li²⁺ and Be³⁺. For multi-electron species satisfactory results are not obtained.

4.1 POSTULATES

1. In any atom, electrons can rotate only in certain selected (or permissible) orbits without radiating energy. Such orbits are known as non-radiating orbits or stationary states. These orbits are circular with well-defined radii. These orbits are numbered 1, 2, 3, …. (from the nucleus). Orbits are paths of revolution of electrons. A spherical surface around the nucleus which contains an orbit of equal energy and radius is called a shell. The shells are denoted as K, L, M, N, …..
2. Each stationary state (or orbit) corresponds to a certain energy level (i.e., as long as the electron is in the particular stationary state it has a definite amount of energy). The energy associated with an electron is least in the K-shell and it increases as we pass to higher L, M, N, ….. shells.
3. An electron can jump from one stationary state to another. For an electron to jump from an lower orbit of energy E₁ to a higher orbit of energy E₂ it should absorb the equivalent of a quantum of energy = E₂ – E₁ = hν, where ν is the frequency of radiation absorbed. Similarly, when it jumps back from the outer to the inner orbit, it will emit an equal amount of energy in the form of an electromagnetic radiation.
4. When an electron absorbs energy, it passes from an inner to an outer orbit; then the electron or the atom is said to be in an excited state. An excited electron must always fall back to a lower orbit within a very short interval of time and as it does so, it releases the quantum of energy absorbed during excitation.
5. The angular momentum of an electron moving in a stationary state is quantized. The angular momentum of an electron moving in a circular orbit is mvr, where m is the mass, v, the velocity and r, the radius of the electronic orbit. According to Bohr, angular momentum of an orbit is given by

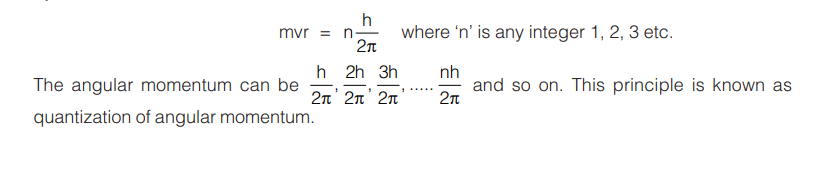
SECTION 5 : HYDROGEN EMISSION SPECTRUM

Spectral lines are associated with electronic transitions. Hydrogen atom contains only one electron and its spectrum is the simplest to analyse. The spectrum of atomic hydrogen consists of a number of discrete lines in the UV, visible and IR regions. Each line corresponds to a particular frequency or wavelength.

The space between two lines represents the frequency range in which no radiation is emitted by the hydrogen atom.

Lines observed in the atomic spectra of hydrogen are grouped into several series called the spectral series. (Refer to the table given below).

A group of lines appearing in the UV region is called the Lyman series; that in the visible region is called the Balmer series. In the IR region, there are three : Paschen, Brackett and Pfund series.

The wave number of any line in a particular series (say Balmer) of a given atom (say hydrogen) can be represented as a difference of two terms, one of which is a constant and the other variable throughout the series. This statement is called the Ritz combination principle (i.e., a combination of 2 terms).

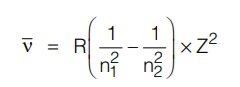
When n₁ and n₂ are integers (n₂ > n₁) and R is called the Rydberg Constant g Constant for g Constant hydrogen. For the Balmer series of hydrogen specifically n₁ = 2 and n₂ is a higher orbit, also value of Z = 1 for hydrogen.

Spectral Series for Hydrogen

Series	n1	n2	Spectral Region
Lyman	1	2, 3, 4 …..	UV
Balmer	2	3, 4, 5 …..	Visible
Paschen	3	4, 5, 6 …..	IR
Brackett	4	5, 6, 7 …..	IR
Pfund	5	6, 7, 8 …..	IR

SECTION 6 : DUAL NATURE OF MATTER AND RADIATION

From the study of wave like and particle like characteristics of the light, scientists came to the conclusion that light and other electromagnetic radiations have dual nature. These are of wave nature as well as particle nature.

Certain phenomenon like interference and diffraction could be explained on the basis of the wave nature while a few others like black body radiations and photoelectric effect could be explained by particle nature. The dual nature of the radiations formed the basis of the modern picture of the atomic model. Some of these revolutionary experiments are discuss herewith.

6.1 de BROGLIE EQUATION

Louis de Broglie suggested that matter in general and electrons in particular exhibit dual character. They behave both as waves as well as particles and hence electron, like radiations, has dual character (wave and particle nature).

de Broglie gave a relation for calculating the wavelength of the wave associated with a particle of mass ‘m’ moving with velocity ‘v’ as given below :

The electron microscope is constructed on the basis of de Broglie’s concept. The electron has been regarded as a tiny, negatively charged material particle revolving in fixed orbits. But Davisson and Germer showed that when a beam of electrons is allowed to fall on the face of a nickel crystal, it gets diffracted, a property peculiar to wave-like radiation. The wave associated with a moving material particle is hence called a matter-wave.

Davisson and Germer’s Experiment

In 1927, Clinton Davisson and Lester Germer fired slow moving electrons at crystalline nickel target. The angular dependency of the reflected electron intensity was measured and was determined to have the same diffraction pattern as those predicted for X-rays by Bragg. Only electromagnetic radiations were believed to show diffraction as they were waves. Diffraction patterns exhibited by electrons confirmed the De-Broglie’s hypothesis that material objects moving with a velocity must possess a characteristic wavelength.

De-Broglie wavelength in terms of kinetic energy of particles:

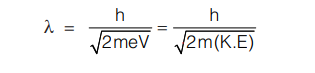
6.2 PHOTOELECTRIC EFFECT

When a clean metallic surface in vacuum is irradiated with monochromatic light, electrons are emitted from the metal. This is called photoelectric effect.

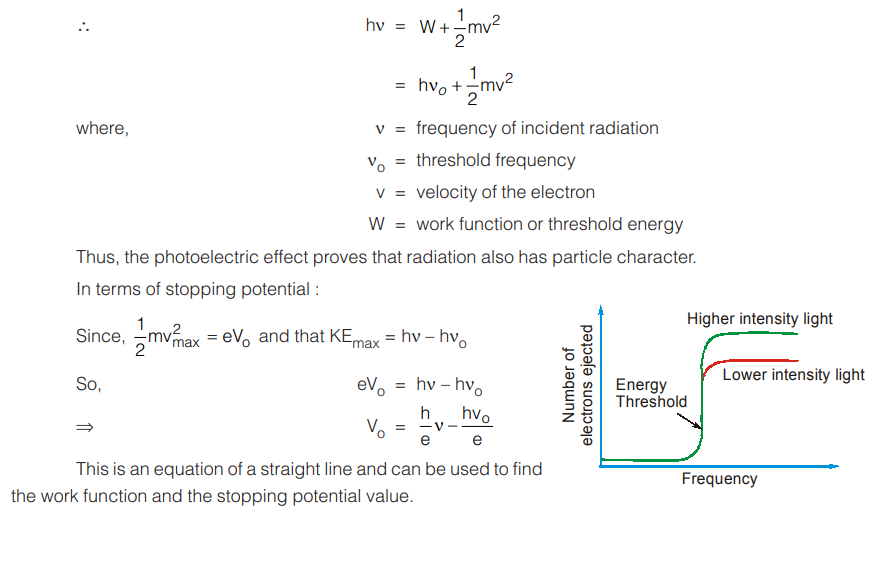
It is found that the kinetic energy of the emitted electrons increases linearly with the frequency of incident light.

If the frequency is below a critical value (called threshold frequency ν₀ (or) work function) no emission of electron is observed. This frequency ν₀ is characteristic of the metal.

It is also observed that increasing the intensity of radiation has no effect on the kinetic energy of photoelectrons. It only increases the number of photoelectrons emitted.

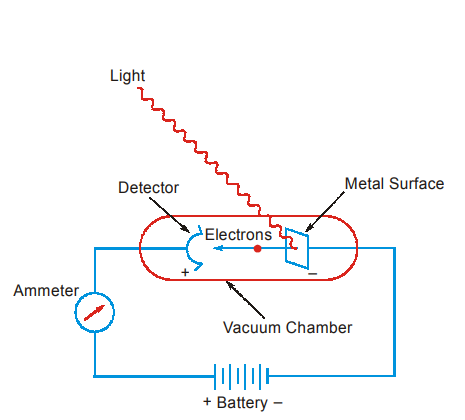
In the Max Planck’s explanation, the energy of the photon is proportional to the frequency. When a photon strikes the metallic surface, it gives up its energy to the electron. Part of the energy is used to release the electron from the metal and the remaining becomes the kinetic energy of the electron released.

SECTION 7 : QUANTUM NUMBERS

These are useful to explain the position, energy of an electron and atomic spectra of atoms.

7.1 PRINCIPAL QUANTUM NUMBER (n)

1. Proposed by Bohr.
2. Determines the size of an atom and energy of the electron.
3. These numbers are given by 1, 2, 3, 4 (or) by the letters K, L, M, N.
4. The energy of electron increases with increase of the principal quantum number value.

7.2 AZIMUTHAL OR SUBSIDIARY OR ANGULAR MOMENTUM QUANTUM NUMBER (l)

(i) Proposed by Sommerfeld. (ii) Determines the three-dimensional shape of the electron cloud (orbital) and sub-shells present in a shell. The l value ranges from zero to n – 1. Example : First orbit (n = 1) l value is zero. If n = 2, then l values are 0, 1. (iii) If l = 0 → ‘s’ sub-shell. If l = 1 → ‘p’ sub-shell. If l = 2 → ‘d’ sub-shell. If l = 3 → ‘f’ sub-shell. (iv) The energy of any sub-shell is equal to (n + l). (v) The order of energies of the sub-shell in main energy level is s < p < d < f. (vi) The relation between orbital angular momentum of an electron and azimuthal quantum number

7.3 MAGNETIC QUANTUM NUMBER (m)

(i) Proposed by Lande. (ii) Determines the orientation of an orbital in space with respect to the standard set of coordinate axis. (iii) Explains Zeeman effect and Stark effect. (iv) The magnetic quantum number values ranges from –l to +l including zero. If l = 0 (s-orbital) contains only one orbital (2 × 0 + 1). If l = 1 (p-orbital) contains 2 × 1 + 1 = 3 orbitals. (iv) The number of orbitals in sub-energy level are given by magnetic quantum number and is given by (2l + 1). (vi) The maximum number of electrons present in a sub-shell is given by 2(2l + 1).

7.4 SPIN QUANTUM NUMBER (s)

• Proposed by Uhlenbeck and Goudsmith.
• Represents the spin of an electron around its own axis in an orbital.

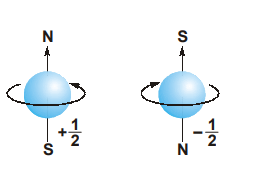
• The possible spin quantum number values of an electron are given

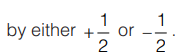
• The two electrons present in an orbital have different spin quantum number values (i.e., the electrons are paired).
• Spin multiplicity = (2s + 1) where s = Total Spin. The number of electrons present in orbit = 2n² (n = principal quantum number). Example : The number of electrons present in L-shell (n = 2) = 2 × 2² = 8.

The number of orbitals present in an orbit = n².

Example : First orbit (n = 1) contains only one orbital.

For n^th energy level, the maximum number of sub-shells = n; orbitals = n²; electrons = 2n².

SECTION 8 : SHAPES OF ATOMIC ORBITALS

8.1 s-ORBITAL

An electron is considered to be smeared out in the form of a cloud. The shape of the cloud is the shape of the orbital. The cloud is not uniform but denser in the region where the probability of finding the electron is maximum.

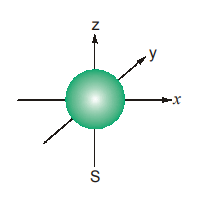
The orbital with the lowest energy is the 1s orbital. It is a sphere with its centre at the nucleus of the atom. The s-orbital is said to be spherically symmetrical about the nucleus, so that the electronic charge is not concentrated in any particular direction. 2s-orbital is also spherically symmetrical about the nucleus, but it is larger than (i.e., away from) the 1s-orbital.

8.2 p-ORBITALS

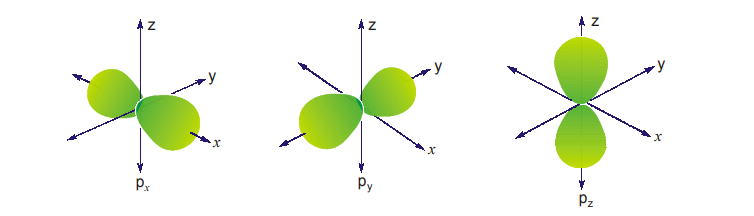
There are three p-orbitals viz., p_x, p_y and p_z. They are dumb-bell shaped the two halves being separated by a nodal plane, i.e., a plane where there is no likelihood of finding the electron. The p-orbitals have a marked directional character, depending on whether p_x, p_y and p_z orbital is being considered. The porbitals consist of two lobes with the atomic nucleus lying between them. The axis of each p-orbital is perpendicular to the other two. The p_x, p_y and p_z orbitals are equivalent except for their directional property. They have the same energy; orbitals having the same energy are said to be degenerate.

8.3 d-ORBITALS

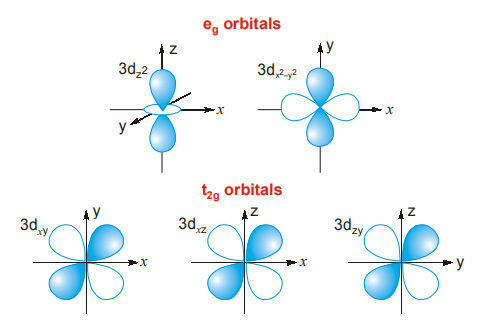
There are five d-orbitals. The shapes of four d-orbitals resemble five four-leaf clovers. -leaf clovers The fifth d-orbital looks like that of a p-orbital. The shapes of these orbitals are given. Each d-orbital is double dumb-bell in shape, i.e., it has 4 lobes. The e_g orbitals (d_x2–_y2 and d_z2) have their lobes lying over the axes whereas t_2g orbitals (d_xy, d_yz, d_zx) have lobes lying in planes.

8.4 f-ORBITALS

There are seven f-orbitals and is said to be sevenfold degenerate. Their shapes are complicated. How the electrons are distributed in the various orbitals of an atom will be given after a study of the position of the element in the Periodic Table.

SECTION 9 : QUANTUM MECHANICAL DESCRIPTIONS OF THE ATOM

9.1 NODE AND NODAL PLANE

Node is defined as a region where the probability of finding an electron is zero. Nodes can be of two types :

• Radial node or spherical node
• Angular node or planar node

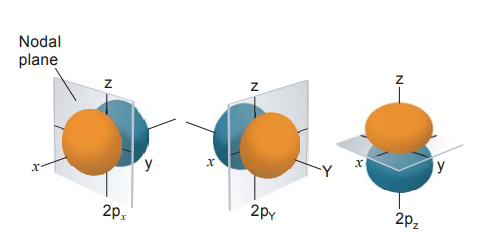
Radial node or spherical node : They correspond to ‘n’ values, i.e., as the distance between nucleus and outermost shell increase, the number of radial nodes increases. For example, 1s, 2p, 3d & 4f orbital are closest to nucleus (∵ 1p, 1d, 2d, 1f, 2f, 3f does not exist) so there is no radial node but for higher values of ‘n’, radial nodes can be defined.

Angular node or planar node : They correspond to ‘l’ value. It depends upon the shape of orbitals. For example, ‘s’ orbitals are spherically symmetrical in all three planes; so in s-orbital, no angular node exists. p-orbitals are not spherically symmetrical but the electron density is concentrated in one plane either x, y or z, so, they have one angular node. Similarly electron density in d-orbital is concentrated in two planes, i.e., xy, yz, zx etc. So the d-orbitals have two angular nodes.

Total number of radial nodes = (n – l – 1)

Total number of angular nodes = l

Total number of nodes = (n – l – 1) + l = n – 1

[Note : If the node at r → ∞ is also considered then number of nodes will be ‘n’ (not n – 1)]

Nodal Plane : This is an infinite plane passing through an orbital, where the probability of finding the electron is zero at each point on the plane. As the s-orbital is spherical in shape, it does not have any nodal plane. The p-orbital has one nodal plane and the d-orbital has two. Overall, the number of nodal planes = l. Remember that the d_z2 orbital does not have any nodal plane due to its unusual shape.

SECTION 10 : ELECTRONIC CONFIGURATION OF AN ATOM

It is the filling up of electrons into various orbitals in an atom following the rules given below. It is given by the notation nl^x.

n = Principal quantum number

l = azimuthal quantum number

x = number of electrons

10.1 AUFBAU PRINCIPLE (THE ORDER OF FILLING OF ELECTRONS)

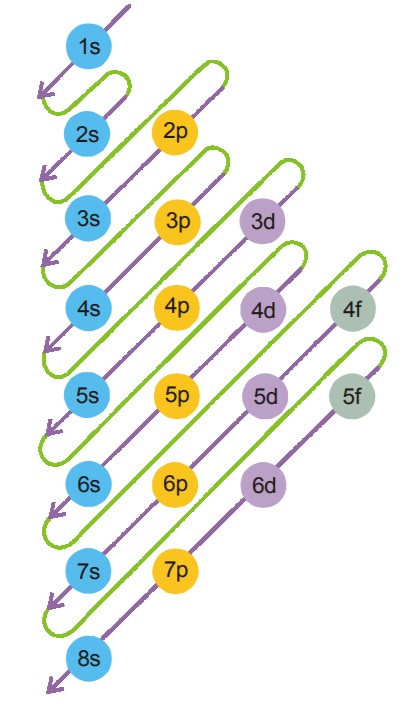1. Electrons tend to occupy orbitals of minimum energy. The orbital (sub-shell) with gy lowest ener lowest energy is filled first filled first. filled first Refer to the diagram given below, fill the 1s orbital first followed by 2s and then 2p and so on.
2. (n + l) rule : The order of increasing energy of the ule : sub-levels in neutral atoms is determined by the order of increasing value of the sum (n + l).

1.  The orbital with lowest (n + lowest (n + l) value is filled first ) value is filled first. ) value is filled first Example: Among 2s, 3s orbitals the electro ns first enter into 2s (whose n + l value is less than that of 3s).
2.  When two sub-levels have the same value of (n + same value l), the sub-level with lower ‘n’ value will be filled first.

Example : For 3p and 4s sub-levels the n + l value is same, i.e., 5. But the electron first enters into 3p sub-level (m = 3).

10.2 HUND’S RULE OF MAXIMUM MULTIPLICITY

Whenever degenerate orbitals (orbitals of same energy) are available, electrons tend to occupy all the orbitals singly with same (parallel) spin before pairing in any one orbital occurs.

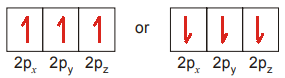
As we know the Hund’s rule, let us see how the three electrons are arranged in p-orbitals.

The important point to be remembered is that all the singly occupied orbitals should haveelectrons with parallel spins, i.e., in the same direction either clock-wise or anticlockwise.

10.3 PAULI’S EXCLUSION PRINCIPLE

No two electrons in an atom can have the same set of four quantum numbers. If follows that in an atom any two electrons may have the same values for any of the three quantum numbers but the fourth must be different.

For example, 2s orbital has n = 2, l = 0, m = 0

This shows that each orbital can carry a maximum of two electrons in opposite spins. Overall, the p-subshell can support six, d-subshell can support 10 and f-subshell can carry 14 electrons.