Thermodynamics

SECTION 1 : SOME BASIC TERMS OF THERMODYNAMICS

1. System : A system is defined as that part of the universe which is under investigation.
2. Surroundings : The part of the universe other than the system is known as surroundings

Universe = System + Surroundings

TYPES OF SYSTEMS

Isolated System : A system that cannot exchange mass and/or energy with the surroundings.  For example : ice, milk or any other liquid kept in a thermos flask.

Closed System : It exchanges only energy with the surroundings. For example :

• Water in closed bottle (boundaries of closed system act as conductor of heat)
• Heating of CaCO₃ in sealed tube, etc.

Open System : It exchanges energy and mass both with the surroundings.

For example : Trees in forest, tea in an open cup, etc.

Macro System : A very large number of molecules/atoms are present in this system. Properties of a macro system are called macro properties.

For example : Pressure, temperature, density, composition, viscosity, surface tension, colour, refractive index, etc.

State of System : The system in which the values of macro properties are definite. It is said to be in definite state. Thus, the state of system is determined by its macro properties.

State Functions : The properties of a system which depend only on initial and final states, and do not depend on its path.

For example : Free energy, enthalpy, internal energy, etc.

Extensive Property : The property which depends on the amount of substance present in the system.

For example : Mass volume, Heat capacity, Entropy, Enthalpy, Free energy, Internal energy etc.

Intensive Property : These do not depend on the amount of substance present in the system.

For example : Temperature, Density, Viscosity, Melting point, Boiling point, Surface tension, Refractive index. etc.

SECTION 2 : THERMODYNAMIC PARAMETERS

HEAT (Q)

The energy transferred from hotter body to colder body is known as heat. If heat is given to the system Q > 0. If heat is released from system Q < 0.

WORK (W)

Work done by system ⇒ W < 0, W = –ve

Work done on the system ⇒ W > 0, W = +ve

Pressure-Volume Work

Consider a cylinder fitted with a frictionless and weightless piston having area of cross section A. Let the pressure acting on the piston be P(external pressure), which is slightly less than the internal pressure of gas. Suppose the gas expands a little and piston is pushed out a small distance dx. The work done by the gas on the piston will be

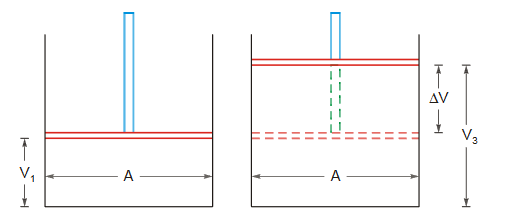
If the volume of gas changes from V₁ to V₂ then total work done W will be given by

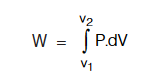
If the external pressure P against which the gas expands remains almost constant throughout the process then

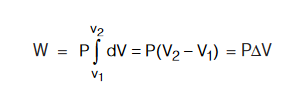According to latest SI convention :

• Work is taken as negative when work is done by the system on the surrounding as in expansion of gas

∆W = –P∆V

• Work is taken as positive when work is done on the system as in contraction of gas

∆W = P∆V

INTERNAL ENERGY

The total energy contained in a system is called its internal energy or intrinsic energy. This is denoted by a symbol E or U. Change in internal energy = ∆E. If internal energy is increased ⇒ ∆E > 0                          [∆E = positive] If internal energy is decreased ⇒ ∆E > 0                         [∆E = negative]

Characteristics of Internal Energy

1. The fixed amount of energy contained in a substance is called its internal energy.
2. Internal energy is present in all the substances.
3. Quantitative Property : Internal energy depends on chemical nature, pressure, temperature and volume of the substance.
4. State Functions : Internal energy depends on the physical state of the system.
5. Internal energy is the total of all types of energy, e.g., potential energy, kinetic energy, vibrational energy, rotational energy, etc.
6. Absolute value of internal energy cannot be determined. Only change in internal energy (∆E) can be determined.

∆E = Energy in final state – Energy in initial state

∆E = E₂ – E₁

∆E = Sum of energy of the products – Sum of energy of reactants

• Internal energy is an extensive property.
• In most stable form, internal energy of the system is regarded as zero.

SECTION 4 : FIRST LAW OF THERMODYNAMICS

Energy can neither be produced nor destroyed, it can only be changed from one form to the other, i.e.,

1. Total energy of an isolated system remains constant.
2. Total energy of universe remains constant.
3. Whenever some amount of any form of energy disappears, the same amount of energy of other form is produced.

MATHEMATICAL FORMULATION OF THE FIRST LAW OF THERMODYNAMICS

Let, Initial internal energy of the system = E₁

Heat supplied to the system = q

Work done on the system = w

Final internal energy of the system = E₂

According first law of thermodynamics

E₂ = E₁ + q + w

E₂ – E₁ = q + w

∆E = q + w

CALCULATION OF WORK DONE (W)

For any expansion against external pressure p_ext ;

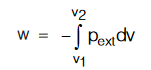
Case 1 : When V is constant (Isochoric process)

w = 0, q_v = ∆E

Case 2 : When p_ext is constant (isobaric process)

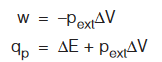
If process is reversible and isobaric, i.e., p_ext = P_gas = constant

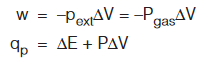
Case 3 : When T is constant (Isothermal expansion)

Case (a) : When process is irreversible isothermal and p_ext is constant.

w = – p_ext∆V

Case (b) : When process is reversible and isothermal.

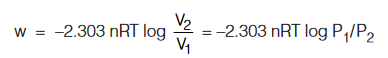
Important Fact : During isothermal expansion for a sample of ideal gas ∆E = 0.

Case 4 : When q = 0, i.e., (adiabatic reversible process)

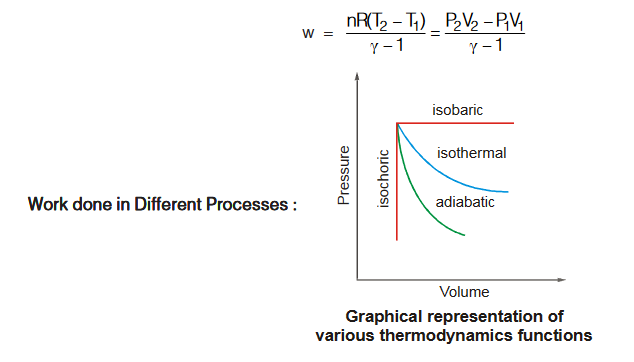
SECTION 6 : ENTROPY (S)

It is a thermodynamic property and is a measure of disorderliness or randomness of a system, i.e., greater the disorder in a system, higher is the entropy of that system.

Solid < Liquid < Gas

Entropy is a state function and does not depend on path.

SOME IMPORTANT POINTS RELATED TO ENTROPY

1. 1. 1. Entropy change, ∆S = S (Final state) – S (Initial state)
      2. Among states of matter, entropy of solid > liquid > gas.
      3. Reactions involving increase in overall moles generally show increase in entropy.
      4. When a solute gets dissolved a solvent, the entropy increases.
      5. When the number of gaseous products increases in a chemical reaction, the entropy also increases. For example.

   (NH₄)₂S (s) → 2NH₃ (g) + H₂S (g)

   6. NH₃ (g) + HCl (g) → NH₄Cl (s) Entropy is decreasing.
   7. For a reaction, change in entropy ∆S = Sum of entropies of the products – Sum of entropies of the reactants.
   8. From the formula given above, unit of entropy is Joule kelvin^–1 mole^–1.
   9. At equilibrium, ∆S_universe for the process is zero.

SECTION 7 : SECOND LAW OF THERMODYNAMICS

1. The first law of thermodynamics does not help us to predict the direction of the change. The answer to this problem is provided by second law of thermodynamics. The statement of the law is developed in terms of the entropy criterion.
2. The second law of thermodynamics introduces the concept of entropy and its relation with spontaneous processes.
3. In an isolated system such as mixing of gases, there is no exchange of energy or matter between the system and the surroundings. But due to increase in randomness, there is increase in entropy. Thus, we can say that for a spontaneous process in an isolated system, the change in entropy is positive. i.e., ∆S > 0.
4. However, if the system is not isolated, we have to take into account the entropy changes of the system and the surroundings. Then, the total entropy change (∆S_total) will be equal to the sum of the change in entropy of the system (∆S_system) and the change in entropy of the surroundings (∆S_surrounding), i.e.,

∆S_total = ∆S_system + ∆S_surroundings

5. For a spontaneous process, ∆S_total must be positive, i.e.,

∆S_total = ∆S_system + ∆S_surroundings > 0

6. But system and surroundings constitute universe for thermodynamic point of view so that for spontaneous change

∆S_universe > 0

STATEMENT OF SECOND LAW OF THERMODYNAMICS

This states that the entropy of the universe always increases in every spontaneous (natural) change.

Thus, combining the first and second law of thermodynamics, the combined statement becomes :

The energy of the universe is conserved whereas the entropy of the universe always increases in any natural process.

SECTION 8 : SPONTANEOUS PROCESSES

This type of physical and chemical change occurs of its own under specific circumstances or on proper initiation.

Examples :

1. Flow of liquids from higher to lower level.
2. Flow of gases from higher pressure to lower pressure.
3. Conduction of heat from hot body to the colder body.
4. Flow of electric current from higher potential to lower potential.
5. Dissolution of sugar in water.
6. All naturally occurring processes.
7. Burning of coal and other fuels.

SOME IMPORTANT POINTS RELATED TO SPONTANEOUS CHANGES

• These changes occur only in single direction. They do not occur in opposite direction by themselves. For example. water does not flow itself from lower to upper level.
• Work can be done by a spontaneous change. For example, motion of a piston by expansion of gas, rotation of a wheel when water falls on it from some height, etc.
• For a spontaneous change for an isolated system, ∆S is positive.
• When system is not isolated.

∆S_(total) = ∆S_(system) + ∆S_{(surrounding)} > 0

• Change in entropy of a system

∆S_{(Surroundings)} = q (Reversible)/T

SECTION 9 : FREE ENERGY (G)

The available amount of energy during the process in the system which can be changed into maximum useful work, is called free energy of the system.

Thus, free energy change in the system (∆G), is the measure of the capability of doing useful work by the system.

G = H – TS (Gibbs-Helmholtz equation)

At constant temperature Gibb’s free energy change

∆G = ∆H – T∆S

If   ∆G < 0, then the reaction is spontaneous

∆G = 0, reaction has achieved quilibrium

∆G > 0, then the reaction is non-spontaneous

FREE ENERGY CHANGE AND THE NATURE OF PROCESS

DH	DS	DG = DH – TDS	Remarks
–	(+)	(–) always	Spontaneous
+	+	(+) at low temperature (–) at high temperature	Non-spontaneous Spontaneous
–	–	(–) at high temperature (+) at low temperature	Spontaneous Non spontaneous

SECTION 10 : THERMOCHEMISTRY

Thermochemical Standard State : In thermodynamics, standard state of a substance at a specified temperature is its most stable, pure form at 1 bar pressure.

For example, the standard state of liquid water at 300 K is pure liquid water at 300 K and 1 bar. For example, for the combustion of 1 mol of methane under standard conditions, at 298 K we write the equation

CH₄(g) + 2O₂(g) → CH₄(g) + 2H₂O (l), ∆H (298 K) = –890.4 kJ mol^–1

Thermochemical Equations : A balanced chemical reaction together with the value of heat (energy) evolved or absorbed (i.e., value of ∆H) during reaction is called a thermochemical equation.

Example : C₂H₅OH (l) + 3O₂ (g) → 2CO₂ (g) + 3H₂O (l) ; ∆H = –1367 kJ mol^–1

Conventions regarding Thermochemical Equations : In writing thermochemical equations, the following conventions are followed :

1. For exothermic reaction, ∆H = –ve and for endothermic reaction, ∆H = +ve.
2. The coefficients in a thermo chemical equation refer to the number of moles of reactants and products involved in the reaction.
3. When a chemical equation is reversed, the value of is reversed in sign. For example

N₂ (g) + O₂ (g) → 2NO (g); ∆H = +180.0 kJ mol^–1

2NO₂ (g) → N₂ (g) + O₂ (g); ∆H = –180.0 kJ mol^–1

4. If the coefficients of the substances involved in a reaction are multiplied or divided by certain factor, then the value of ∆H is also treated in the same way, but unit of ∆H will remain kJ mol^–1 . For example,

2P (s) + 3Br₂ (l) → 2PBr₃ (g); ∆H = –243.0 kJ mol^–1

5. The physical states of the different reactants and products must be indicated because the value of ∆H changes with the change in the physical states. For examples ;

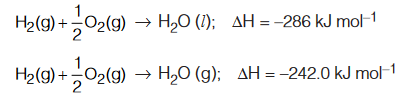
6. The allotropic form of substances must be indicated because the value of ∆H also depends upon allotropic form of substances used. For example,

C (graphite) + O₂ (g) → CO₂ (g); ∆H^θ = –94.0 kJ mol^–1

C (diamond) + O₂ (g) → CO₂ (g); ∆H^θ = –94.5 kJ mol^–1

Standard Enthalpy Changes of Reaction : Standard enthalpy of reaction is the enthalpy change for a reaction when all the participating substances (elements and compounds) are in their standard states. It is denoted by symbol.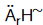

Example : The reaction,

H₂ (g) + Cl₂ (g) → 2HCl (g) ; ∆H = –44.0 kcal,

indicates that when 1 mole hydrogen (2 g hydrogen) in its standard state completely reacts with 1 mole chlorine (71 g chlorine) in its standard state to form 2 mole HCl (73 g HCl) in its standard state, the amount of heat evolved is 44.0 kcal or the enthalpy decreases by 44.0 kcal or the reacting system loses 44.0 kcal of heat or the standard enthalpy change of the reaction, i.e.,

∆H = – 4.0 kcal

SECTION 11 : HESS’S LAW OF CONSTANT HEAT SUMMATION

This law states that, if a reaction is the sum of two or more constituent reactions, then ∆H (enthalpy change) for the overall process must be sum of the ∆H’s of the constituent reactions. In other words, the enthalpy change for a reaction is the same whether it occurs in one step or in a series of steps.

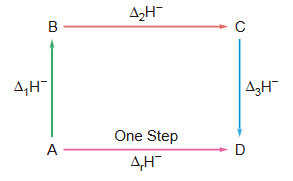
Example : Let us consider a chemical change in which ‘A’ changes into ‘D’. If this change, A → D, can take place either in one step or in more than one step as shown in figure. Then according to Hess’s law, we can write

∆r H^– = ∆₁H + ∆₂H

Hess’s law can be verified experimentally with the help of following examples.

Formation of CO₂ from Carbon

First Method : Carbon is directly converted into CO₂ (g)

C (s) + O₂ (g) → CO₂ (g);        ∆_rH = –393.5 kJ mol^–1

Second Method : Carbon is first converted into CO (g) and then CO (g) into CO₂ (g), i.e., conversion has been carried in two steps.

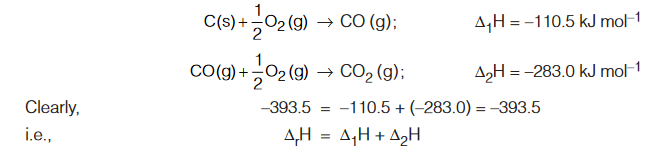
Conclusions Drawn from Hess’s Law

1. Enthalpy change of a reaction (∆_rH) is independent of the path followed, i.e., enthalpy is a state function.
2. ∆_rH is independent of the time consumed in the process.
3. Thermochemical equation can be added, subtracted or multiplied like algebraic equations.

Applications of Hess’s Law

1. The enthalpies of formation of many compounds cannot be determined experimentally. These are calculated by the application of Hess’s law. It can be explained by following example.

Determination of Enthalpies of Slow Reactions like ∆H of Transition

Elements like carbon, sulphur, phosphorus etc., exist in different allotropic form. The enthalpy of transition is the change in enthalpy when one mole of allotropic form of a substance change to the other and vice versa.

The change is very slow and the amount of heat energy exchanged is so small that the value cannot be determined experimentally. However, enthalpies of such transitions can be determined by Hess’s law as explained by following example.

SECTION 12 : BOND ENERGY OR BOND ENTHALPY

The amount of energy required to break one mole of bond of a particular type between the atoms in the gaseous state, i.e., to separate the atoms in the gaseous state under 1 atm. pressure and the specified temperature is called bond dissociation energy.

Example :

H – H (g) → 2H (g);       ∆H = +433 kJ mole^–1

Cl – Cl (g) → 2Cl (g);      ∆H = +242.5 kJ mole^–1

H – Cl (g) → H(g) + Cl (g); ∆H = +431 kJ mole–1

The bond dissociation energy of a diatomic molecule is called bond energy. When more than one bond of the same kind are present in a compound, then the average bond dissociation energy required to break each bond in a compound is called bond energy.

Example : Dissociation of H₂O molecule

H₂O (g) → H (g) + OH (g);     ∆H = 497.8 kJ mole^–1

OH (g) → H (g) + O (g);          ∆H = 428.5 kJ mole^–1

The average bond dissociation energy gives the value of O – H.

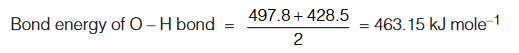
Application of Bond Energy

1. Heat of Reactions : Enthalpy of reaction = ∑Bond energies of reactants – ∑ Bond energies of products
2. Determination of Resonance Energy : When a compound shows resonance there is considerable difference between the heat of formation as calculated from bond energies and that determined experimently. Resonance Energy = Experimental or actual heat of formation – Calculated heat of formation.