Motion in a Straight Line

REST AND MOTION

An object is said to be in motion with respect to an observer, if its position changes w.r.t. that observer. It may happen by both ways either observer moves or object moves.

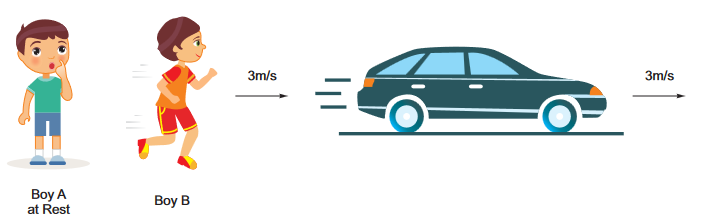
• Boy B is in motion w.r.t. ground but boy B is at rest w.r.t. moving car,
• Boy A is at rest w.r.t. ground but boy A is in motion w.r.t. boy B or moving car.

Position, Distance and Displacement

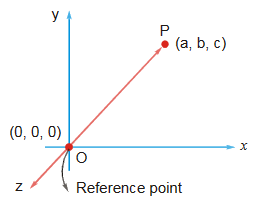
Position: Location of an object at any instant of time is known as its position with respect to a reference point.

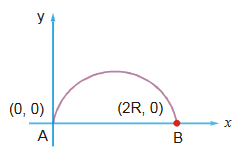
Distance: Actual length of the path travelled by an object in a given interval of time is known as distance travelled. Distance is defined in terms of magnitude only; no direction is associated with distance. So it’s a Scalar quantity.

Actual length of path = πR

Displacement: Shortest distance between the initial and final position of the particle in a particular direction is known as displacement. Displacement is defined with magnitude as well as direction. So it’s a Vector quantity.

The subscripts i and f refer to the initial and final positions. These are not necessarily the positions from which the particle starts its motion nor where its motion ceases. The i and f designate the particular initial and final positions we are considering out of the entire motion of the object

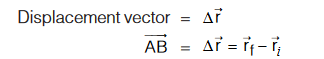
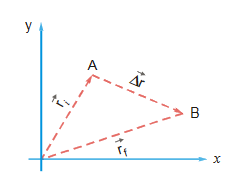
| Displacement | ≤ Distance : Magnitude of displacement is always less than or equals to distance travelled. For a particle moving in a straight line without changing its direction magnitude of displacement and distance becomes equal.

Average and Instantaneous Velocity

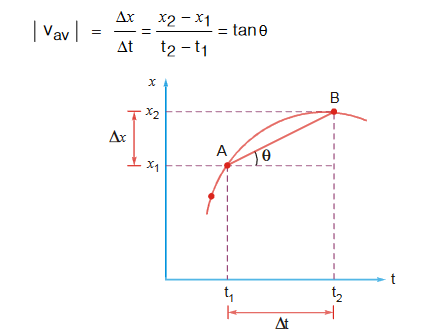
Average Velocity: Change in position of a particle w.r.t. a finite interval of time is known as average velocity of that interval.

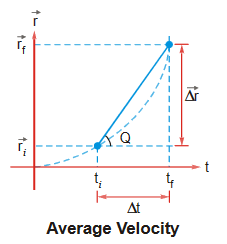
Slope of secant of displacement vs. time graph gives average velocity.

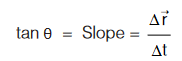
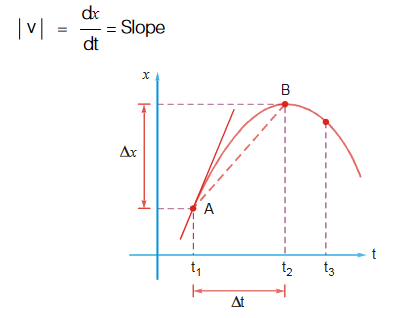
Instantaneous Velocity : Change in position of a particle w.r.t. an infinitesimally small interval of time is known as instantaneous velocity of that instant. Limit of average velocity as the ∆t becomes infinitesimally small is known as instantaneous velocity.

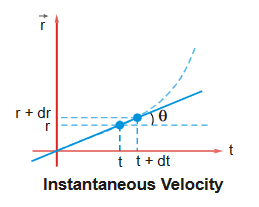
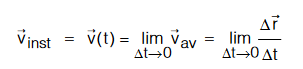
Infinitesimally small means it approaches to zero. When limit approaches to zero than it converts into derivative of r w.r.t. t

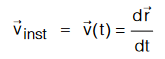
Slope of tangent of displacement vs time graph gives instantaneous velocity.

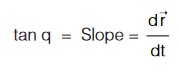
Average and Instantaneous Speed

Average speed is defined as total distance travelled by a particle divided by the total time taken.

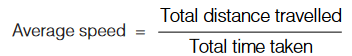
Instantaneous speed is equals to the magnitude of Instantaneous velocity.

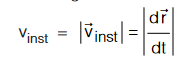
Cases of Average Speed

Let initial speed of an object is v 1, final speed is v2 and acceleration is constant, then

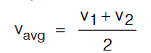
• A body covers a distance s₁ in time t₁, s₂ in time t₂ and s₃ in time t₃.

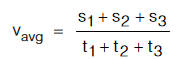
• A body travels with speed v₁ for a time t₁, v₂ for time t₂ and v₃ for the time t₃.

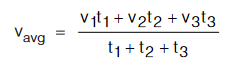
• A body covers a distance s₁ with speed v₁, s₂ with speed v₂ and s₃ with speed v₃.

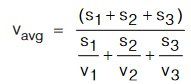A boy goes from home to school with speed v₁ and come back to home with speed v₂. Here distance covered by the boy is same. Time taken by the boy from home to school

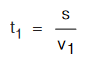
and time taken by the boy from school to home

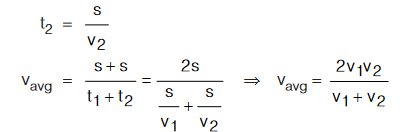
If an object covered one third distance with speed u, next one third with speed v and last one third distance with speed w then,

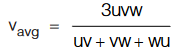
Average and Instantaneous Acceleration

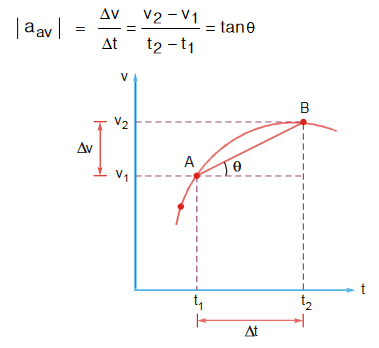
Average acceleration: Rate of change of velocity w.r.t. a time interval is known as average acceleration.

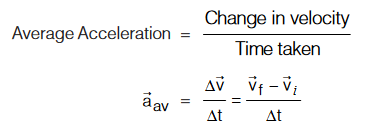
Instantaneous acceleration: Acceleration at a particular instant of time during its motion is known as instantaneous acceleration, it is given as the limit of average acceleration at any time interval ∆t approaches to zero.

Derivative of velocity w.r.t. time is known as instantaneous acceleration.

KINEMATICS

Kinematics Equations For Uniformly Accelerated Motion

If a particle is accelerated with constant acceleration for an interval of time, then the motion is termed as uniformly accelerated motion in that interval of time.

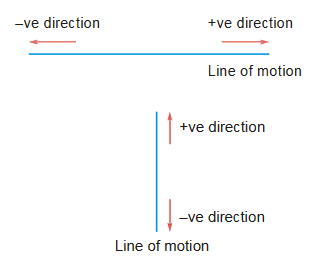
Sign Conventions for Vectors in Straight Line Motion

Since the motion is on straight line, each vector has two possible directions at a particular time instant. You can choose any one direction as positive and the opposite direction as negative.

For example :

1. A particle is moving in horizontal direction (say along x-axis). If the vectors directed towards right are taken as positive then the vectors directed towards left are taken as negative.
2. Similarly, for a particle moving in vertical direction, (say along y-axis) the vectors directed upward may be taken as positive and thus, those directed downwards will be negative.
3. For motion along inclined plane or any other arbitrary direction, if the vectors directed up the plane are positive, then the vectors directed down the plane are negative. You can take any direction of motion as +ve direction and the direction opposite to that becomes negative direction.

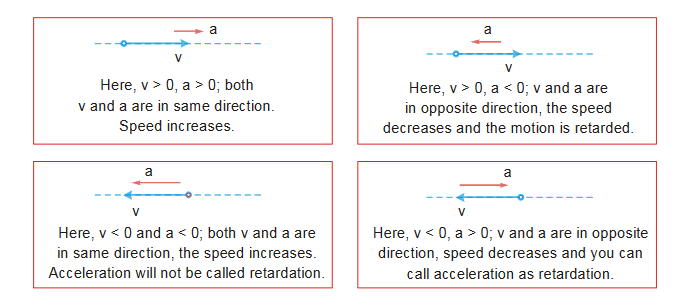
Difference between Acceleration and Retardation

When the speed of a particle decreases or when the particle slows down, the motion is said to be under deceleration or retardation. The necessary requirement for retardation is that the velocity (v) and acceleration (a) should be opposite in direction.

Motion Under Gravity

Suppose a particle is thrown with speed u (vertically upward)

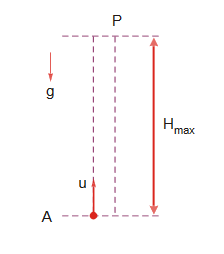
The above results can be easily calculated by equations of motion.

GRAPHS

Position (x) vs Time (t) graph

• Average Velocity:

 

• Instantaneous Velocity :

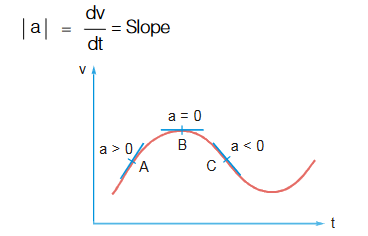
Velocity (v) vs Time (t) graph

• Average Acceleration :

• Instantaneous Acceleration :

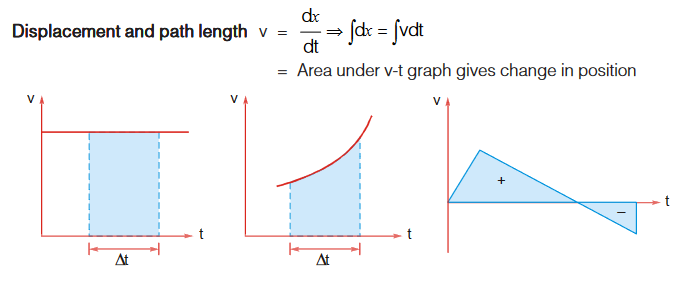
Velocity (v) vs Time (t) graph

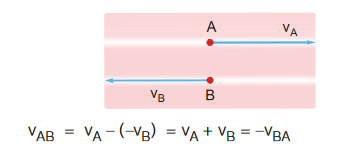
RELATIVE VELOCITY

Velocity, position, acceleration all are frame dependent quantities. All of them can be calculated with respect to a frame or reference point

RELATIVE VELOCITY

Velocity, position, acceleration all are frame dependent quantities. All of them can be calculated with respect to a frame or reference point

 

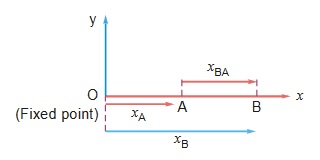
So with the above discussion we concluded that, if A and B are moving along the same direction then,

If A and B are moving in opposite directions